|
|
$1.$ $y = {x^4} + m{x^2} - (m + 1)x - (m + 1)\,\,\,\,\, \Rightarrow y' = 4{x^3} + 2mx - (m + 1)$
Với $x = 1$ thì $y’ = m+3$. Do đó tiếp tuyến của $(C_m$) tại $x = 1$ có phương trình:
$y = (m+3)(x - 1)$
Như vậy ($C_m$) sẽ tiếp xúc với $y = 2(x – 1)$ tại $x = 1 \Leftrightarrow m+3=2 \Leftrightarrow m=-1.$
Khi $m = -1:$
$y=x^4-x^2$
* TXĐ: $D=R$
* Sự biến thiên:
$\mathop {\lim }\limits_{x \to +\infty }y=\mathop {\lim }\limits_{x \to +\infty }x^4 \left ( 1-\frac{1}{x^2} \right )=+\infty $
$\mathop {\lim }\limits_{x \to -\infty }=+\infty $
$y'=4x^3-2x=2x(2x^2-1)$
$y'=0 \Leftrightarrow \left[ \begin{gathered} x=0 \\ x=\pm \frac{1}{\sqrt{2} } \end{gathered} \right. $
BBT:
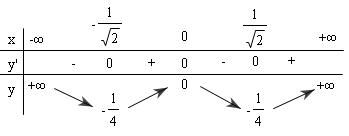
- Hàm số đồng biến trên $ \left ( -\frac{1}{\sqrt{2} }; 0 \right ) $ và $ \left ( \frac{1}{\sqrt{2} }; + \infty \right ) $
- Hàm số nghịch biến trên $ \left ( - \infty ;- \frac{1}{\sqrt{2} } \right ) $ và $ \left ( 0; \frac{1}{\sqrt{2} } \right ) $
- Hàm số đạt cực đại tại $x=0, y_{CĐ}=0$
- Hàm số đạt cực tiểu tại $x= \pm \frac{1}{\sqrt{2} }, y_{CT}=-\frac{1}{4} $
* Đồ thị:
$\cap Ox:$ $x^4-x^2=0 \Leftrightarrow x^2(x^2-1)=0$
$ \Leftrightarrow \left[ \begin{gathered} x=0 \\ x= \pm 1 \end{gathered} \right. $
Đồ thị giao với Ox tại $(0;0); (-1;0); (1;0)$
$\cap Oy: (0;0)$
Ta có: $y(-x)=(-x)^4-(-x)^2$
$=x^4-x^2=y(x)$
Hàm số đã cho là hàm số chẵn $\Rightarrow $ đồ thị nhận Oy làm trục đối xứng.
Vẽ đồ thị:
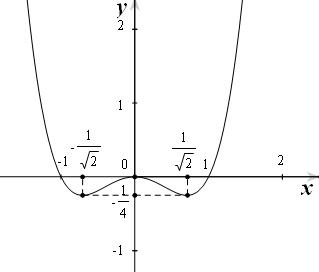
$2.$ $(C_m)$ qua $A(x,y,)\forall m\Leftrightarrow y=x^4+mx^2-(m+1)x-(m+1),\forall m$
$\Leftrightarrow (x^2-1)m+x^4-1-y=0,\forall m$
$\begin{cases}x^2-1=0 \\ x^4-1-y=0 \end{cases} \Leftrightarrow \begin{cases}x=\pm1 \\ y=0 \end{cases} $
Vậy $(C_m)$ luôn đi qua $(-1;0)$ và $(1;0)$
$3.$ Ta có: $4{x^2}(1 - {x^2}) = 1 - k \Leftrightarrow {x^4} - {x^2} = \frac{{k - 1}}{4}$
Số nghiệm pt bằng số giao điểm đường thẳng $y = \frac{{k - 1}}{4}\,\,\,\,(d)$ với đồ thị hàm số $y=x^4-x^2(C)$
Vậy với $\frac{k-1}{4}< -\frac{1}{4}\Leftrightarrow k<0 \,\,(d) $ không cắt $(C) \Rightarrow $ phương trình vô nghiệm
* $-\frac{1}{4}< \frac{k-1}{4}<0 \Leftrightarrow 0<k<1\,\,(d)$ cắt $(C)$ tại 4 điểm phân biệt $\Rightarrow $ phương trình có 4 nghiệm.
* $\frac{k-4}{4}=0 \Leftrightarrow k=1 \,\,\,(d)$ cắt $(C)$ tại 3 điểm phân biệt $\Rightarrow $ phương trình có 3 nghiệm.
* $\left[ \begin{gathered} k=0 \\ \frac{k-1}{4}>0 \end{gathered} \right.\Leftrightarrow \left[ \begin{gathered} k=0 \\ k>1 \end{gathered} \right. \,\,(d) $ cắt $(C)$ tại hai điểm phân biệt $\Rightarrow $ phương trình có hai nghiệm phân biệt.
|