|
|
1.Hàm số $y = \frac{{{\text{ax}} + b}}{{cx + d}}\,\,\,\,(c \ne 0\,\,\& \,\,ad - bc \ne 0)$
Ví dụ: Khảo sát hàm số biến thiên và vẽ đồ thị của hàm số $y = \frac{{{\text{2x}} - 1}}{{x - 1}}$
Giải :
1) Hàm số có tập xác định là $\mathbb{R}\backslash \left\{ 1 \right\}$
2) Sự biến thiên của hàm số
a) Giới hạn vô cực , giới hạn tại vô cực và các đường tiệm cận ta có
$\mathop {\lim }\limits_{x \to {1^ - }} y = - \infty $ và $\mathop {\lim }\limits_{x \to {1^ + }} y = + \infty $ do đó, đường thẳng $x = 1$ là tiệm cận đứng của đồ thị hàm số đã cho ( khi $x \to {1^ - }$ và khi$x \to {1^ + }$)
Vì $\mathop {\lim }\limits_{x \to + \infty } y = \mathop {\lim }\limits_{x \to - \infty } y = 2$ nên đường thẳng $y = 2$ là tiệm cận ngang của đồ thị hàm số đã cho (khi $x \to + \infty $ Và khi$x \to - \infty $)
b) Bảng biến thiên
Ta có $y' = \frac{{ - 1}}{{{{(x - 1)}^2}}} < 0$ với mọi $x \ne 1$
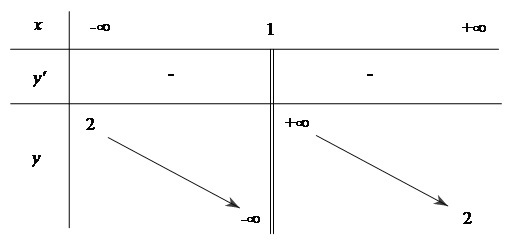
Hàm số nghịch biến trên mỗi khoảng $( - \infty ;1)$ và $(1; + \infty )$
3) Đồ thị:
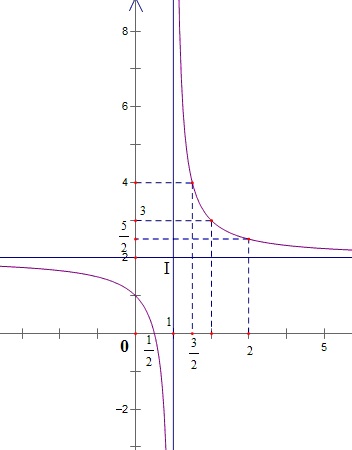
Đồ thị cắt trục tung tại điểm $( 0 ; 1)$ và cắt trục hoành tại điểm $\left( {\frac{1}{2};0} \right)$
Nhận xét: Đồ thị nhận giao điểm $I(1 ; 2)$ của hai đường tiệm cận làm tâm đối xứng.
2 . Hàm số $y = \frac{{{\text{a}}{{\text{x}}^2} + bx + c}}{{a'x + b'}}\,\,\,\,\,\,\,\,(a \ne 0\,,\,\,a' \ne 0)$
Ví dụ: Khảo sát sự biến thiên và vẽ đồ thị của hàm số $y = \frac{{{{\text{x}}^2} - 2x - 3}}{{x - 2}}$
Giải :
Có thể viết hàm số đã cho dưới dạng
$y = x + \frac{3}{{x - 2}}$
1) Hàm số có tập xác định là $\mathbb{R}\backslash \left\{ 2 \right\}$
2) Sự biến thiên của hàm số
a) Giới hạn vô cực , giới hạn tại vô cực và các đường tiệm cận
Ta có
$\mathop {\lim }\limits_{x \to - \infty } y = - \infty $ và $\mathop {\lim }\limits_{x \to + \infty } y = + \infty $
$\mathop {\lim }\limits_{x \to {2^ - }} y = + \infty $ và $\mathop {\lim }\limits_{x \to {2^ + }} y = - \infty $
do đó , đường thẳng x = 2 là tiệm cận đứng của đồ thị hàm số đã cho ( khi $x \to {2^ - }$ và khi$x \to {2^ + }$)
Vì $y - x = \frac{{ - 3}}{{x - 2}} \to 0$ khi $x \to + \infty $ Và khi$x \to - \infty $ nên đường thẳng y = x là tiệm cận xiên của đồ thị hàm số đã cho (khi $x \to + \infty $ Và khi$x \to - \infty $)
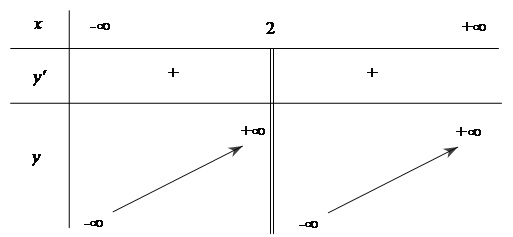
b) Bảng biến thiên
Vì $y' = 1 + \frac{3}{{{{(x - 2)}^2}}} > 0$ với mọi $x \ne 2$ nên hàm số đồng biến trên mỗi khoảng
$( - \infty ;2)$ và $(2; + \infty )$
3) Đồ thị :

Đồ thị cắt trục tung tại điểm $( -1 ; 0)$ và cắt trục hoành tại điểm $\left( {3;0} \right)$
Nhận xét: Đồ thị hàm số nhận giao điểm $I(2 ; 2)$ của hai đường tiệm cận làm tâm đối xứng.
|