a) Đường thẳng $AB$ đi qua điểm $A$ và có vecto chỉ phương $\overrightarrow{a}=(1;3;-1) $
Đường thẳng $\Delta $ đi qua điểm $M_0(5;0;-4)$ và có vecto chỉ phương $\overrightarrow{b}=(2;1;-2) $
Ta có: $[\overrightarrow{a}, \overrightarrow{b} ]=(-5;0;-5), \overrightarrow{AM}_0=(3;-1;-3) $
Suy ra $[\overrightarrow{a}, \overrightarrow{b} ].\overrightarrow{AM}_0 =0$
Vậy hai đường thẳng $AB$ và $\Delta $ đồng phẳng, Ngoài ra hai vecto $\overrightarrow{a}, \overrightarrow{b} $ không cùng phương nên hai đường thẳng $AB$ và $\Delta $ cắt nhau
Đường thẳng $AB$ có phương trình tham số: $\left\{ \begin{array}{l} x=2+t\\ y=1+3t\\z=-1-t \end{array} \right. (t\in R)$
Gọi $I$ là giao điểm của đường thẳng $AB$ và $\Delta $.
Tọa độ của $I$ ứng với $t$ là nghiệm đúng của phương trình
$\left\{ \begin{array}{l} (2+t)-2(1+3t)-5=0\\ (2+t)+2(1+3t)+2(-1-t)+3=0 \end{array} \right. \Leftrightarrow t=-1$
Suy ra $I(1;-2;0)$
Ta có: $\overrightarrow{IA}=(1;3;-1), \overrightarrow{IB}=(3;9;-3) \Rightarrow \overrightarrow{IA}, \overrightarrow{IB} $ cùng hướng. Vậy hai điểm $A, B$ nằm cùng một phía đối với $\Delta $
b) Phương tình của $(\alpha )$ qua $A$ và vuông góc với $\Delta : 2(x-2)+1(y-1)-2(z+1)=0\Leftrightarrow 2x+y-2z-7=0$
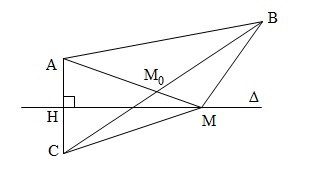
Gọi $H$ là trung điểm của $AC$ thì $H$ là hình chiếu vuông góc của $A$ trên đường thẳng $\Delta $. Tọa độ của $H$ là nghiệm đúng của hệ phương trình:
$\left\{ \begin{array}{l} x-2y-5=0\\ x+2y-2z+3=0\\2x+y-2z-7=0 \end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} x=\frac{23}{9} \\ y=-\frac{11}{9} \\z=-\frac{14}{9} \end{array} \right. \Rightarrow H(\frac{23}{9};-\frac{11}{9};-\frac{14}{9} )$
$\Rightarrow C(\frac{28}{9};-\frac{32}{9};-\frac{19}{9} )$
Do $A$ và $C$ là hai điểm đối xứng qua đường thẳng $\Delta $ nên với $M$ là một điểm bất kì trên $\Delta $ ta có: $MA=MC$. Do đó: $MA+MB=MC+MB\geq BC$
Đẳng thức xảy ra khi ba điểm $B,C,M$ thẳng hàng. Khi đó $M$ trùng với $M_0$ là giao điểm của $BC$ và đường thẳng $\Delta $:
Đường thẳng $BC$ có vecto chỉ phương $\overrightarrow{v}=(4;47;-4) $
phương trình tham số của đường thẳng $BC:\left\{ \begin{array}{l} x=4+4t\\ y=7+47t\\z=-3-4t \end{array} \right. (t\in R)$
Giao điểm $M_0$ của $\Delta $ và $BC$ ứng với $t$ là nghiệm của hệ phương trình:
$\left\{ \begin{array}{l} (4+4t)-2(7+47t)-5=0\\ (4+4t)+2(7+47t)+2(-3-4t)+3=0 \end{array} \right. \Rightarrow t=-\frac{1}{6} $
Suy ra $M_0(\frac{10}{3};-\frac{5}{6};-\frac{7}{3} )$
Vậy $\max(MA+MB=BC)=\sqrt{\frac{322}{3} } $ khi $M$ ở vị trí $M_0(\frac{10}{3};-\frac{5}{6};\frac{7}{3} )$