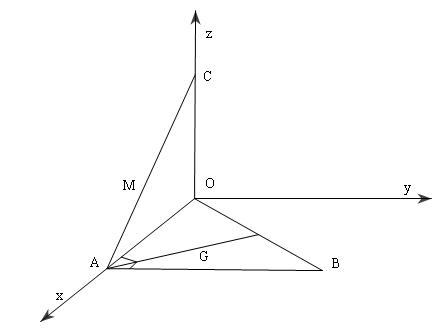
a. Xác định điểm C trên Oz để thể tích OABC=8
Theo giả thiết ta có OA=4,OB=8, góc AOB=600
⇒ΔAOB vuông tại A⇒BA⊥Ox⇒x0=xA=4. Ta được B(4,y0,0)
Vì OB=8⇒42+y20=64⇒y0=4√3⇒AB=4√3
VOABC=13OC.SΔAOB=13OC.8√3=8⇔OC=√3
Do đó SΔABO=12OA.OB=12.4.4√3=8√3
Ta được C(0,0,√3) hoặc C(0,0,−√3)
b.Ta có trọng tâm của ΔOAB là G(83,4√33,0)
Giả sử C(0,0,√3);→AC=(−4,0,√3)
⇒ Phương trình đường thẳng AC là {x=4−4ty=0z=√3t
Ta được M(4−4t,0,√3t)⇒→OM(4−4t;0;√3t)
→GM=(43−4t;−4√33;√3t)
Thế thì OM⊥GM⇔→OM.→GM=0
⇔(4−4t).(43−4t)+3t2=0⇔57t2−64t+16=0
⇔t=32±4√757⇔M(4−1657(8±√7),0,4√357(8±√7))
Trường hợp còn lại ứng với C(0,0,−√3) cũng tương tự ⇔M(4−1657(8±√7),0,−4√357(8±√7)