|
|
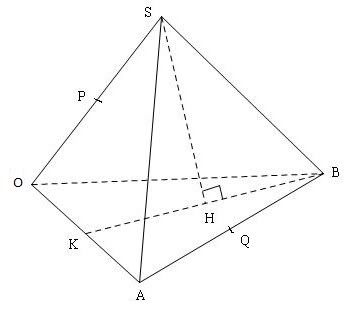
$1.$ $\overrightarrow {BS}=(2,-4,7),
\overrightarrow {OA} =(6,3,0) \Rightarrow \overrightarrow {SB.} \overrightarrow {OA}=0\Rightarrow \overrightarrow {SB} \bot \overrightarrow {OA} $
$2.$ Kẻ $SH\bot (OAB)$
$\Rightarrow SH\bot OA;SB\bot OA\Rightarrow OA\bot (SKB)$
$\Rightarrow OA\bot BK$
$\overrightarrow {OA} =(6,3,0)=\overrightarrow {n} $
$\Rightarrow $ mặt phẳng $(SBK)$ có phương trình $2x+y-5=0$
Phương trình $OA$
$\begin{cases}x=2t \\ y=t \\z=0\end{cases} $
Thế vào phương trình $(SBK)\Rightarrow t=1 \Rightarrow K(2,1,0)$
$3.$ $P(0,\frac{5}{2} ,4); Q(2,6,\frac{1}{2} )$
$\overrightarrow {PK} =(2,-\frac{3}{2},-4 )//(4,-3,-8)$
$\overrightarrow {QK}=(0,-5,-\frac{1}{2} ) //(0,10,1)$
$\Rightarrow $ vectơ pháp tuyến của $(PQK)$ : $[(4;-3;-8);(0;10;1)]=(77;-4;40)$
Mặt phẳng $(PQK)$ có phương trình : $77x-4y+40z-150=0$
$\overrightarrow {SB} =(-2,4,-7)\Rightarrow $ đường thẳng $SB$ có phương trình
$x=2t,y=-4t+5,z=7t+8$.
Thế vào phương trình mặt phẳng $(PQK)\Rightarrow t=-\frac{1}{3} $
$\Rightarrow $ điểm $M$ có tọa độ $(-\frac{2}{3},\frac{19}{3},\frac{17}{3}) $
|