Bài 101756

Question

Trong không gian có hệ tọa độ Đề các vuông góc

$Oxyz$ cho hình lập phương

$ABCDA'B'C'D'$ với

$A'(0, 0, 0), B'(0, 2, 0), (2, 0, 0), A'(0, 0, 2)$ . Gọi

$M, N, P, Q$ theo thứ tự là trung điểm các đoạn

$D'C', C'B', B'B, AD$ .

$1$ . Tìm tọa độ hình chiếu của điểm

$C$ trên

$AN$

$2$ . Chứng tỏa rằng

$2$ đường thẳng

$NP, MQ$ cùng nằm trong một mặt phẳng và tính diện tích tứ giác

$MNPQ$ .

hoàng anh thọ · Answer 1 · 4/27/2012 10:17:09 AM

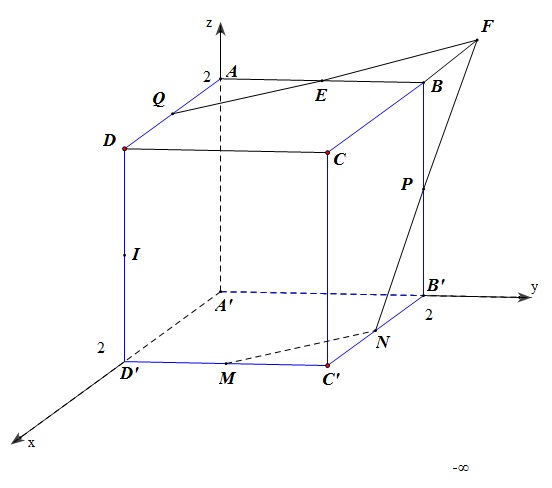
$1$ . Từ giả thiết

$\Rightarrow$

$A(0, 0, 2)$ và

$N(1, 2,0)$

$\Rightarrow \overrightarrow {AN} = \left( {1,\,2,\, - 2} \right)$ ,đường thẳng

$AN$ có phương trình tham số

$\left\{ \begin{array}{l} x = t\\ y = 2t\\ z = 2 - 2t \end{array} \right.$ . Điểm

$C$ có tọa độ

$(2, 2, 2)$
Xét điểm

$H\left( {t,\,2t,\,2 - 2t} \right)\, \in AN$ , ta có

$\overrightarrow {CH} = \left( {t - 2,\,2t - 2,\, - 2t} \right)$ .

$H$ là hình chiếu vuông góc của

$C$ xuống

$AN$

$\Rightarrow \overrightarrow {CH} .\overrightarrow {AN} \, = \,0\, \Leftrightarrow \,t - 2 + 4t - 4 + 4t = 0 \Leftrightarrow \,t = \frac{2}{3}$ . Vậy

$H$ có tọa độ

$\left( {\frac{2}{3},\,\frac{4}{3},\,\frac{2}{3}} \right)$ .

$2$ .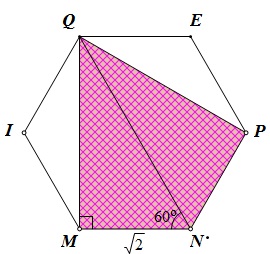

Gọi

$E$ là trung điểm của

$AB$ thì

$QE \parallel DB \parallel D'B' \parallel MN$

$\Rightarrow$

$M; N; Q; E$ thuộc cùng một mặt phẳng

$\left( \alpha \right)$ ;

$QE$ cắt

$CB$ ở

$F$ và ta có

$BF = \,EB\, = \,BP\, \Rightarrow \,\Delta BPF\, = \Delta B'PN\, \Rightarrow$

$N, P, F$ thẳng hàng;

$M, N, P, F, E, Q$

$\in$

$\left( \alpha \right) \Rightarrow$

$MQ, NP$ đồng phẳng.
Gọi

$I$ là trung điểm của

$AD$ thì dễ chứng minh

$I$

$\in \left( \alpha \right)$ và đa giác

$MNPEQI$ là một lục giác đều có cạnh

$MN = \frac{1}{2} B'D' = \frac{1}{2}.2\sqrt 2 = \sqrt 2$ .
Ta có:

$S(MNPQ) = 2S(MQN) = 2.\frac{1}{2}MN.MQ = MN.MN.\tan {60^\circ} = M{N^2}.\sqrt 3 = 2\sqrt 3$ (đvdt)

Bài 101756

1 Đáp án

Lý thuyết liên quan

Bài 101756

1 Đáp án

Liên quan

Lý thuyết liên quan