|
|
a. Ta có hình vẽ sau:
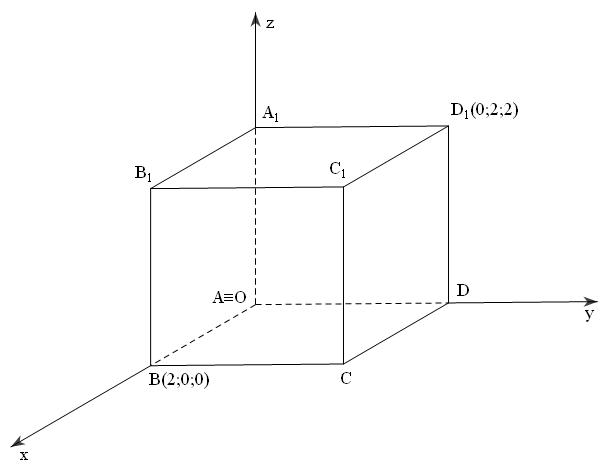
Ta có $A\left( {0,0,0} \right);B\left( {2,0,0} \right);C\left( {2,2,0} \right)$;D(0;2;0); ${A_1}\left( {0,0,2} \right);{B_1}\left( {2,0,2} \right);{C_1}\left( {2,2,2} \right);{D_1}\left( {0,2,2} \right)$
Mp $\left( {A{B_1}{D_1}} \right)$ có cặp VTCP là: $\overrightarrow {A{B_1}} = \left( {2,0,2} \right)$; $\overrightarrow {A{D_1}} = \left( {0,2,2} \right)$
nên mp $\left( {A{B_1}{D_1}} \right)$ có 1 PVPT là $\overrightarrow u = \frac{1}{4}\left[ {\overrightarrow {A{B_1}} ,\overrightarrow {A{D_1}} } \right] = \left( { - 1, - 1,1} \right)$
Ta có $M\left( {2,1,0} \right)$ nên Mp $\left( {AM{B_1}} \right)$ có cặp VTCP là: $\overrightarrow {AM} = \left( {2,1,0} \right)$; $\overrightarrow {A{B_1}} = \left( {2,0,2} \right)$
nên mp $\left( {AM{B_1}} \right)$ có 1 VTPT là $\overrightarrow v = \frac{1}{2}\left[ {\overrightarrow {AM} ,\overrightarrow {AB} } \right] = \left( {1, - 2, - 1} \right)$
Ta có: $\overrightarrow u .\overrightarrow v = - 1\left( 1 \right) - 1\left( { - 2} \right) + 1\left( { - 1} \right) = 0 \Leftrightarrow \overrightarrow u \bot \overrightarrow v \rightarrow \left( {A{B_1}{D_1}} \right) \bot \left( {AM{B_1}} \right)$ (đpcm)
b. ${\overrightarrow {AC} _1} = \left( {2,2,2} \right)$ nên phương trình tham số $A{C_1}:\left\{ \begin{array}{l}
x = t\\
y = t\\
z = t
\end{array} \right.$, $N \in A{C_1} \Rightarrow N\left( {t,t,t} \right)$
Phương trình $\left( {A{B_1}{D_1}} \right): - \left( {x - 0} \right) - \left( {y - 0} \right) + \left( {z - 0} \right) = 0 \Leftrightarrow x + y - z = 0$
$d\left( {N,(A{B_1}{D_1})} \right) = \frac{{\left| {t + t - t} \right|}}{{\sqrt 3 }} = \frac{{\left| t \right|}}{{\sqrt 3 }} = {d_1}$
Phương trình $\left( {AM{B_1}} \right):\left( {x - 0} \right) - 2\left( {y - 0} \right) - \left( {z - 0} \right) = 0 \Leftrightarrow x - 2y - z = 0$
$ \Rightarrow d\left( {N,(AM{B_1})} \right) = \frac{{\left| {t - 2t - t} \right|}}{{\sqrt {1 + 4 + 1} }} = \frac{{\left| { - 2t} \right|}}{{\sqrt 6 }} = {d_2}$
\rightarrow $\frac{{{d_1}}}{{{d_2}}} = \frac{{\frac{{\left| t \right|}}{{\sqrt 3 }}}}{{\frac{{2\left| t \right|}}{{\sqrt 6 }}}} = \frac{{\left| t \right|}}{{\sqrt 3 }}\frac{{\sqrt 6 }}{{2\left| t \right|}} = \frac{{\sqrt 6 }}{{2\sqrt 3 }} = \frac{{\sqrt 2 }}{2}$
Vậy tỉ số khoảng cách từ $N \in A{C_1}\left( {N \ne A \Leftrightarrow t \ne 0} \right)$ tới 2 mặt phẳng $\left( {A{B_1}{D_1}} \right)$ và $\left( {AM{B_1}} \right)$ không phụ thuộc vào vị trí của điểm N.
|