Bất phương trình đã cho tương đương với:
$-1<\frac{x^2+3x-1}{x^2+x-2} <1 \Leftrightarrow \begin{cases}\frac{x^2+3x-1}{x^2+x-2} >-1 (1)\\ \frac{x^2+3x-1}{x^2+x-2} <1 (2)\end{cases} $
Giải $(1)$: $(1) \Leftrightarrow \frac{x^2+3x-1}{x^2+x-2} +1>0 \Leftrightarrow \frac{2x^2+4x-3}{x^2+x-2}>0 $
Tam thức $2x^2+4x-3$ có hai nghiệm $x=-\frac{2 \pm \sqrt{10} }{2} $
Tam thức $x^2+x-2$ có hai nghiệm $x=1; x=-2$
Lập bảng xét dấu phân thức vế trái của bất phương trình , ta có:

Nghiệm của (1) là:
$S=\left\{ {x | x \in \mathbb{R}; x< \frac{-2- \sqrt{10} }{2} }; -2<x< \frac{-2+\sqrt{10} }{2}; x>1 \right\} $
Giải $(2)$: $(2) \Leftrightarrow \frac{x^2+3x-1}{x^2+x-2} -1<0 \Leftrightarrow \frac{2x+1}{x^2+x-2}<0 $
Lập bảng:
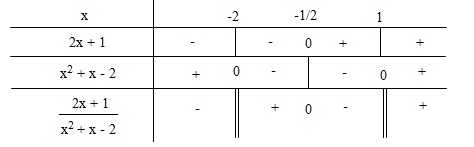
Nghiệm của $(2): S=\left\{ {x | x \in \mathbb{R}; x<-2; -\frac{1}{2}<x<1 } \right\} $
Kết hợp nghiệm của $(1)$ và $(2)$:

Nghiệm của bất phương trình đã cho:
$S=\left\{ {x | x \in \mathbb{R}; x< \frac{-2-\sqrt{10} }{2}; -\frac{1}{2}<x<\frac{-2+ \sqrt{10} }{2} } \right\} $.