|
|
$1/$ Hàm số xác định trên đoạn $\left[ {\frac{1}{2},\,4} \right]$
Ta có $f(x) = \left\{ \begin{array}{l}
{y_1} = - {x^2} - 2x + 3 + \frac{3}{2}\ln
x\,\,\,\,\,\,\,\,\,\,\,\,\,\frac{1}{2} \le x \le 1\\
{y_2} = {x^2} + 2x - 3 + \frac{3}{2}\ln x\,\,\,\,\,\,\,\,\,\,\,\,\,\,1 \le x \le 4
\end{array} \right.$
* Với $\frac{1}{2} \le x \le 1:\,\,\,\,\,\,\,{f^ / }\left( x \right) = {y_1}^ / = - 2x - 2 +
\frac{3}{{2x}}$
${f^ / }\left( x \right) = \frac{{\left( { - 2x + 1} \right)\left( {2x + 3}
\right)}}{{2x}} < 0\,\,\,\,\,\,\,\,\,\,\forall x \in \left[ {\frac{1}{2},1} \right]$
* Với $1 \le x \le 4:\,\,\,\,\,\,{f^ / }\left( x \right) = {y_2}^ / = 2x + 2 + \frac{3}{{2x}} >
0\,\,\,\,\forall x \in \left[ {1,4} \right]$
Ta có $f\left( {\frac{1}{2}} \right) = \frac{7}{4} - \frac{3}{2}\ln 2$
$\begin{array}{l}
f(1)\,\,\,\,\, = 0\\
f(4)\,\,\,\, = 21 + 3\ln 2
\end{array}$
Bảng biến thiên:
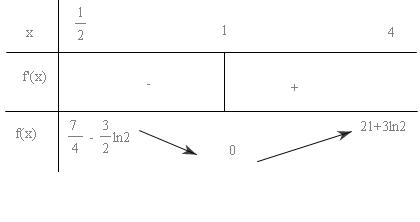
Bảng biến thiên cho thấy : $\mathop {Maxf(x)}\limits_{\frac{1}{2} \le x \le 4} = 21 + 3\ln 2$
$\mathop {\min f(x)}\limits_{\frac{1}{2} \le x \le 4} = 0$
$2)$ ĐS : $\mathop {Maxf(x)}\limits_{\frac{1}{2} \le x \le 2} = 4 + \ln 2$
$\mathop {Maxf(x)}\limits_{\frac{1}{2} \le x \le 2} = 0$
|