|
|
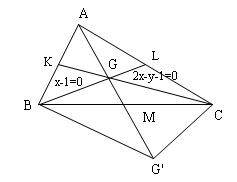
Gọi K,L,M lần lượt là trung điểm của các cạnh AB,AC,BC
Thay tọa độ của A(3,1) vào phương trình các trung tuyến 2x−y−1=0 và x−1=0 ta được 2.3−1−1≠0 và 3−1≠0
Vậy điểm A không nằm trên hai trung tuyến đã cho.
Gọi trung tuyến xuất phát từ C là 2x−y−1=0 và trung tuyến xuất phát từ B là x−1=0
Trọng tâm G là nghiệm của hệ phương trình :
{2x−y−1=0x−1=0⇒G(1;1)
Gọi G′ là điểm đối xứng của G qua trung điểm M của cạnh BC.
Ta có : AG=2GM suy ra AG=GG′ và G là trung điểm AG′.Gọi (x;y) là tọa độ của G′
xG=xA+xG′2=1⇒1=3+xG′2⇒xG′=−1
yG=yA+yG′2=1⇒1=1+yG′2⇒yG′=1
BGCG′ là hình bình hành (vì GB//CG' và CG//G'B)
BG'//CK nên phương trình BG' có dạng 2x-y+C=0
BG' qua G'(-1,1) nên -2-1+C=0\Rightarrow C=3
Phương trình BG' là 2x-y+3=0
B là giao điểm của hai đường thẳng BL và BG' nên tọa độ B là nghiệ của hệ :
\begin{cases}2x-y+3=0 \\ x-1=0 \end{cases} \Rightarrow B(1;5)
G'C//BL nên phương trình G'C có dạng x+C=0
G'C qua G'(-1,1)\Rightarrow -1+C=0\Rightarrow C=1
Phương trình G'C là x+1=0
Đỉnh C là giao điểm của hai đường thẳng CK, G'C nên tọa độ C là nghiệm của hệ :
\begin{cases}2x-y-1=0 \\ x+1=0 \end{cases} \Rightarrow C(-1,-3)
Đường thẳng AB qua A(3,1), B(1;5) có phương trình :
\frac{x-3}{1-3} =\frac{y-1}{5-1} \Rightarrow 2x+y-7=0
Đường thẳng AC qua A(3,1), C(-1,-3) có phương trình :
\frac{x-3}{-1-3}=\frac{y-1}{-3-1}\Rightarrow x-y-2=0
Đường thẳng BC qua B(1,5), C(-1,-3) có phương trình :
\frac{x-1}{-1-1}=\frac{y-5}{-3-5}\Rightarrow 4x-y+1=0
|