|
|
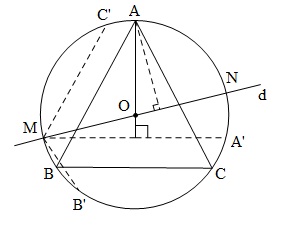
Cách 1 : Giả sử $\Delta ABC$ đều, nội tiếp đường tròn $\left( {O;R} \right)$, đường thẳng $d $ qua $O$ cắt đường tròn tại $M$ và $N$. Gọi các điểm đối xứng của $M$ qua $OA, OB, OC$ lần lượt là $A’, B’, C’$.
Ta có do đó $\Delta A'B'C'$ đều.
Mặt khác, các khoảng cách từ $A,B,C$ đến $d$ tương ứng bằng các khoảng cách từ $M$ đến $OA,OB,OC$ và do đó, tương ứng bằng nửa các khoảng cách từ M đến $A',B',C'$. Kết hợp với Bài 103290 , ta có tổng bình phương các khoảng cách từ $A,B,C$ đến $d$ bằng
$\frac{1}{4}\left( {M{A^{'2}} + MB{'^2} + MC{'^2}} \right) = \frac{1}{4}6{R^2} = \frac{3}{2}{R^2}$
Cách 2 : trước hết ta sẽ chứng minh.
${\cos ^2}\left( {\overrightarrow {OM} ,\overrightarrow {OA} } \right) + {\cos ^2}\left( {\overrightarrow {OM} ,\overrightarrow {OB} } \right) + {\cos ^2}\left( {\overrightarrow {OM} ,\overrightarrow {OC} } \right) = $không đổi.
Không ảnh hưởng đến tính tổng quát ta có thể coi $R = 1$, tức là $|\overrightarrow {OA} | = |\overrightarrow {OB} | = |\overrightarrow {OC} | = |\overrightarrow {OM} | = 1$
Giả sử $\overrightarrow {OM} = \alpha \overrightarrow {OA} + \beta \overrightarrow {OB} + \gamma \overrightarrow {OC} $ với $\alpha + \beta + \gamma = 1$
Ta có $1 = {\overrightarrow {OM} ^2} = {\alpha ^2} + {\beta ^2} + {\gamma ^2} + 2\left( {\alpha \beta \overrightarrow {OA} .\overrightarrow {OB} + \beta \gamma \overrightarrow {OB} .\overrightarrow {OC} + \gamma \alpha \overrightarrow {OC} .\overrightarrow {OA} } \right)$
$\begin{array}{l}
= {\alpha ^2} + {\beta ^2} + {\gamma ^2} - \left( {\alpha \beta + \beta \gamma + \gamma \alpha } \right)\\
= {\left( {\alpha + \beta + \gamma } \right)^2} - 3\left( {\alpha \beta + \beta \gamma + \gamma \alpha } \right)\\
= 1 - 3\left( {\alpha \beta + \beta \gamma + \gamma \alpha } \right)\\
\Rightarrow \alpha \beta + \beta \gamma + \gamma \alpha = 0\\
\Rightarrow {\alpha ^2} + {\beta ^2} + {\gamma ^2} = 1
\end{array}$
Khi đó :
$\begin{array}{l}
{\cos ^2}\left( {\overrightarrow {OM} ,\overrightarrow {OA} } \right) + {\cos ^2}\left( {\overrightarrow {OM} ,\overrightarrow {OB} } \right) + {\cos ^2}\left( {\overrightarrow {OM} ,\overrightarrow {OC} } \right) = \\
= {\left( {\overrightarrow {OM} .\overrightarrow {OA} } \right)^2} + {\left( {\overrightarrow {OM} .\overrightarrow {OB} } \right)^2} + {\left( {\overrightarrow {OM} .\overrightarrow {OC} } \right)^2}\\
= {\left[ {\left( {\alpha \overrightarrow {OA} + \beta \overrightarrow {OB} + \gamma \overrightarrow {OC} } \right).\overrightarrow {OA} } \right]^2} + {\left[ {\left( {\alpha \overrightarrow {OA} + \beta \overrightarrow {OB} + \gamma \overrightarrow {OC} } \right).\overrightarrow {OB} } \right]^2}\\ +
{\left[ {\left( {\alpha \overrightarrow {OA} + \beta \overrightarrow {OB} + \gamma \overrightarrow {OC} } \right).\overrightarrow {OC} } \right]^2}
\end{array}$
$\begin{array}{l}
= {\left( {\alpha - \frac{1}{2}\beta - \frac{1}{2}\gamma } \right)^2} + {\left( {\beta - \frac{1}{2}\gamma - \frac{1}{2}\alpha } \right)^2} + {\left( {\gamma - \frac{1}{2}\alpha - \frac{1}{2}\beta } \right)^2}\\
= \frac{1}{4}\left[ {{{\left( {2\alpha - \beta - \gamma } \right)}^2} + {{\left( {2\beta - \alpha - \gamma } \right)}^2} + {{\left( {2\gamma - \alpha - \beta } \right)}^2}} \right]\\
= \frac{1}{4}\left[ {6\left( {{\alpha ^2} + {\beta ^2} + {\gamma ^2}} \right) - 6\left( {\alpha \beta + \beta \gamma + \gamma \alpha } \right)} \right]\\
= \frac{1}{4}.6 = \frac{3}{2}
\end{array}$
Trở lại bài toán, tổng bình phương các khoảng cách từ $A,B,C$ đến d bằng
$\begin{array}{l}
O{A^2}.{\sin ^2}\left( {\overrightarrow {OM} ,\overrightarrow {OA} } \right) + O{B^2}.{\sin ^2}\left( {\overrightarrow {OM} ,\overrightarrow {OB} } \right) + O{C^2}.{\sin ^2}\left( {\overrightarrow {OM} ,\overrightarrow {OC} } \right)\\
= {R^2}\left[ {3 - {{\cos }^2}\left( {\overrightarrow {OM} ,\overrightarrow {OA} } \right) - {{\cos }^2}\left( {\overrightarrow {OM} ,\overrightarrow {OB} } \right) - {{\cos }^2}\left( {\overrightarrow {OM} ,\overrightarrow {OC} } \right)} \right]\\
= {R^2}\left( {3 - \frac{3}{2}} \right) = \frac{3}{2}{R^2}
\end{array}$
|
|
|
Đăng bài 07-05-12 10:05 AM
|
|