A. TÓM TẮT LÝ THUYẾT
$1.$ Khái niệm cực trị hàm số:
Giả sử hàm số $f$ xác định trên tập hợp $D (D\subset
\mathbb{R})$ và $x_0\in D$
a) $x_0$ được gọi là một điểm cực đại
của hàm số $f$ nếu tồn tại một khoảng $(a;b)$ chứa điểm $x_0$ sao cho
$(a;b) \subset D$ và $f(x) < f (x_0)$ với mọi $x\in(a;b)\setminus
\left\{ {x_0} \right\}$. Khi đó $f(x_0)$ được gọi là giá trị cực đại của hàm số $f$.
b) $x_0$ được gọi là một điểm cực tiểu của hàm số $f$ nếu tồn
tại một khoảng $(a;b)$ chứa điểm $x_0$ sao cho $(a;b) \subset D$ và
$f(x) > f (x_0)$ với mọi $x\in(a;b)\setminus \left\{ {x_0} \right\}$.
Khi đó $f(x_0)$ được gọi là giá trị cực tiểu của hàm số $f$.
Giá trị cực đại và giá trị cực tiểu được gọi chung là cực trị
Nếu $x_0$ là một điểm cực trị của hàm số $f$ thì người ta nói rằng hàm số $f$ đạt cực trị tại điểm $x_0$.
Như vậy: điểm cực trị phải là một điểm trong của tập hợp $D(D\subset
\mathbb{R})$.
$2$. Điều kiện cần để hàm số đạt cực trị:
Định lý $1$. Giả sử hàm số $f$ đạt cực trị tại điểm $x_0$. Khi đó, nếu $f$ có đạo hàm tại điểm $x_0$ thì $f’(x_0)=0$
Chú ý:
Đạo hàm $f’$ có thể bằng $0$ tại điểm $x_0$ nhưng hàm số $f$ không đạt cực trị tại điểm $x_0$.
Hàm số có thể đạt cực tri tại một điểm mà tại đó hàm số không có đạo hàm.
Hàm số chỉ có thể đạt cực trị tại một điểm mà tại đó đạo hàm của hàm số bằng 0, hoặc tại đó hàm số không có đạo hàm.
$3.$ Điều kiện đủ để hàm số đạt cực trị:
Định lý $2$: Giả sử hàm số $f$ liên tục trên khoảng $(a;b)$ chứa điểm $x_0$ và có đạo hàm trên các khoảng $(a; x_0)$ và $(x_0;b)$. Khi đó
a)
Nếu $\begin{cases}f'(x_0)<0, x\in (a;x_0) \\f'(x_0)>0, x\in
(x_0;b) \end{cases}$ thì hàm số đạt cực tiểu tại điểm $x_0$. Nói một
cách khác, nếu $f’(x)$ đổi dấu từ âm sang dương khi $x$ qua điểm $x_0.$
thì hàm số đạt cực tiểu tại $x_0$.

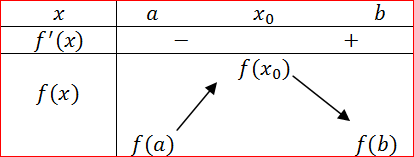
b) Nếu $\begin{cases}f'(x_0)>0, x\in (a;x_0) \\f'(x_0)<0, x\in
(x_0;b) \end{cases}$ thì hàm số đạt cực đại tại điểm $x_0$. Nói một
cách khác, nếu $f’(x)$ từ dương sang âm khi $x$ qua điểm $x_0$ thì hàm số đạt cực đại tại $x_0$.
Định lý $3$. Giả
sử hàm số $f$ có đạo hàm cấp một trên khoảng $(a,b)$ chứa điểm
$x_0,f'(x_0 )=0$ và $f$ có đạo hàm cấp hai khác $0$ tại điểm $x_0.$
a) Nếu $f’’(x_0)<0$ thì hàm số $f$ đạt cực đại tại điểm $x_0.$
b) Nếu $ f’’(x_0)>0$ thì hàm số $f$ đạt cực tiểu tại điểm $x_0.$
$4$. Quy tắc tìm cực trị:
Quy tắc $1$: áp dụng định lý $2$
Tìm $f’(x)$
Tìm các điểm $x_i (i=1,2,3…)$ tại đó đạo hàm bằng $ 0$ hoặc hàm số liên tục nhưng không có đạo hàm.
Xét dấu của $f’(x)$. Nếu $f’(x)$ đổi dấu khi $x$ qua điểm $x_0$ thì hàm số có cực trị tại điểm $x_0.$
Quy tắc $2$: áp dụng định lý $3$
Tìm $ f’(x)$
Tìm các nghiệm $x_i (i=1,2,3…)$ của $f’(x) = 0$
Với mỗi $x_i$ tính $f’’(x_i).$
Nếu $f’’(x_i)<0$ thì hàm số đạt cực đại tại điểm $x_i.$
Nếu $f’’(x_i)>0$ thì hàm số đạt cực tiểu tại điểm $x_i.$
B. VÍ DỤ MINH HỌA
Ví dụ $1$. Tìm cực trị của các hàm số
a) $f(x)=\frac{1}{3}x^3-x^2-3x+\frac{5}{3}$
b) $y=f(x)=|x|(x+2)$
Lời giải :
a) Hàm số đã cho xác định trên $\mathbb{R}$.
Ta có : $f'(x)=x^2-2x-3$
$f'(x)=0\Leftrightarrow
\left[ {\begin{matrix} x=-1\\ x=3\end{matrix}} \right.$
Cách $1.$ Bảng biến thiên
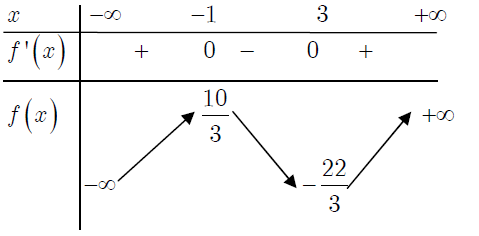
Hàm số đạt cực đại tại điểm $x=-1, f(-1)=\frac{10}{3}$, hàm số đạt cực tiểu tại
điểm $x=3, f(3)=-\frac{22}{3}$.
Cách $2.$ $f''(x)=2x-2$
Vì $f''(-1)=-4<0$ nên hàm số đạt cực đại tại điểm $x=-1, f(-1)=\frac{10}{3}$.
Vì $f''(3)=4>0$ nên hàm số đạt cực đại tại điểm $x=3, f(3)=-\frac{22}{3}$.
b) $f(x)=|x|(x+2)=\begin{cases}x(x+2) \text {khi} x \ge
0\\-x(x+2) \text {khi} x < 0 \end{cases}$
Hàm số đã cho xác định và liên tục trên $\mathbb{R}$.
Ta có : $f'(x)=\begin{cases}2x+2>0 \text {khi} x > 0\\ -2x-2>0
\text {khi} x < 0 \\ 0 \text {khi} x = 0\end{cases}$
Hàm số liên tục tại $x=0$, không có đạo hàm tại $x=0$.
Bảng biến thiên
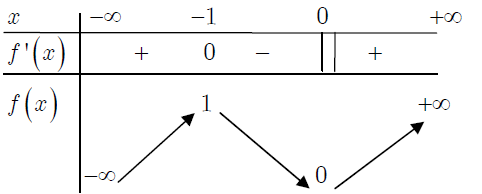
Hàm số đạt cực đại tại điểm $x=-1, f(-1)=1.$
Hàm số đạt cực tiểu tại điểm $x=0, f(0)=0.$
Ví dụ $2$. Tìm cực trị của các hàm số
a) $f(x)=x\sqrt{4-x^2}$
b) $f(x)=8-2\cos x -\cos 2x$
Lời giải :
a) Hàm số đã cho xác định trên $[-2;2]$.
Ta có : $f'(x)=\frac{4-2x^2}{\sqrt{4-x^2}}, x \in (-2;2)$
$f'(x)=0\Leftrightarrow
\left[ {\begin{matrix} x=-\sqrt 2\\ x=\sqrt 2\end{matrix}} \right.$
Bảng biến thiên
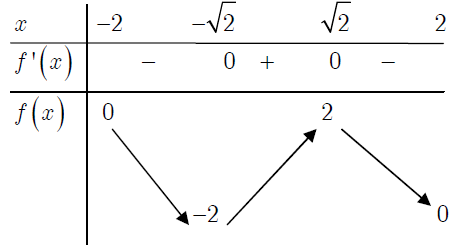
Hàm số đạt cực tiểu tại điểm $x=-\sqrt 2, f(-\sqrt 2)=-2$,
Hàm số đạt cực tiểu tại điểm $x=\sqrt 2, f(\sqrt 2)=2$.
b)
Hàm số đã cho xác định và liên tục trên $\mathbb{R}$.
Ta có : $f'(x)=2\sin x + 2\sin 2x=2\sin x(1+2\cos x)$
$f'(x)=0\Leftrightarrow
\left[ {\begin{matrix}\sin x=0\\ \cos x=-\frac{1}{2} \end{matrix}}
\right.\Leftrightarrow \left[ {\begin{matrix} x=k\pi\\ x=\pm
\frac{2\pi}{3} +k2\pi\end{matrix}} \right. ( k \in
\mathbb{Z})$
$f''(x)=2\cos
x+4\cos 2x$
$f''\left ( \pm
\frac{2\pi}{3} +k2\pi \right )=-3<0$.
Hàm số đạt cực đại tại $x=\pm
\frac{2\pi}{3} +k2\pi,f\left ( \pm \frac{2\pi}{3} +k2\pi \right )=\frac{9}{2}$
$f''\left ( k\pi
\right )=2\cos k\pi +4>0$.
Hàm số đạt cực tiểu tại $x=k\pi,f\left ( k\pi
\right )=2(1-\cos k\pi)$
Bài tập tương tự. Tìm cực trị của các hàm số
a) $f(x)=\sqrt{|x|}(x-3)$
b) $f(x)=|x|$
c) $f(x)=2\sin 2x -3$
d) $f(x)=x-\sin 2x +2$
Đáp số :
a)
Hàm số đạt cực đại tại điểm $x=0, f(0)=0$,
Hàm số đạt cực tiểu tại điểm $x=1, f(1)= -2$.
b)
Hàm số đạt cực đại tại điểm $x=0, f(0)=0$.
c)
Hàm số đạt cực đại tại các điểm $x=\frac{\pi}{4}+k\pi, f\left (
\frac{\pi}{4}+k\pi \right )=-1$,
Hàm số đạt cực tiểu tại điểm $x=\frac{\pi}{4}+(2k+1)\frac{\pi}{2},f\left (
\frac{\pi}{4}+(2k+1)\frac{\pi}{2} \right )=-5$.
Trong đó $k \in \mathbb{Z}.$
d)
Hàm số đạt cực đại tại các điểm $x=-\frac{\pi}{6}+k\pi$,
Hàm số đạt cực tiểu tại điểm $x=\frac{\pi}{6}+k\pi$.
Trong đó $k \in \mathbb{Z}.$
Ví dụ $3$.
a) Với giá trị nào của $m$ thì hàm số $y=f(x,m)=(m+2)x^3+3x^2+mx+m$ có cực đại,
cực tiểu.
b) Với giá trị nào của $m$ thì hàm số $y=f(x,m)=\frac{1}{2}x^4-mx^2+\frac{3}{2}$có
cực tiểu mà không có cực đại.
Lời giải :
a) Hàm số đã cho xác định trên $\mathbb{R}.$
Ta có : $y'=3(m+2)x^2+6x+m$
Hàm số có cực đại và cực tiểu khi phương trình $y'=0$ có hai nghiệm phân biệt
hay
$\begin{cases}m+2 \ne 0 \\ \Delta'=9-3m(m+2)>0\end{cases}\Leftrightarrow
\begin{cases}m+2 \ne 0 \\ m^2+2m-3<0 \end{cases}\Leftrightarrow
\begin{cases}m+2 \ne 0 \\ -3<m<1 \end{cases}$
Vậy giá trị $m$ cần tìm là $-3<m<1, m \ne -2$.
b) Hàm số đã cho xác định trên $\mathbb{R}.$
Ta có : $y'=2x^3-2mx$
$y'=0\Leftrightarrow\left[
{\begin{matrix} x=0\\ x^2=m (*) \end{matrix}} \right.$
Hàm số đã cho có cực tiểu mà không có cực đại khi phương trình $y'=0$ có một
nghiệm duy nhất và $y'$ đổi dấu khi $x$ đi qua nghiệm đó. Khi đó PT $x^2=m
(*)$ vô nghiệm hay có nghiệm kép $x=0\Leftrightarrow m \le 0$.
Vậy $m \le 0$ là giá trị cần tìm.
Bài tập tương tự.
a) Với giá trị nào của $m$ thì hàm số $y=f(x)=x^3+(m+3)x^2+1-m$ đạt cực đại tại
$x=-1$
b) Với giá trị nào của $m$ thì hàm số $y=f(x)=x^3-6x^2+3(m+2)x-m-6$ đạt cực đại
và cực tiểu đông thời hai giá trị này cùng dấu.
Hướng dẫn :
a) Chứng tỏ rằng $f'(x)=0\Leftrightarrow \left[ {\begin{matrix} x=0\\ x=
-\frac{2m+6}{3}\end{matrix}} \right.$
Để suy ra yêu cầu bài toán $\Leftrightarrow -\frac{2m+6}{3}=-1\Leftrightarrow
m=-\frac{3}{2}$
b) Đáp số : $-\frac{17}{4}<m<2$.