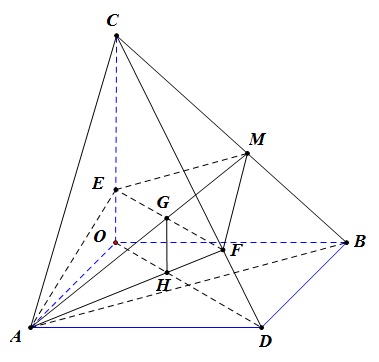
|
|
$1$. Chọn $Oxyz$ làm hệ trục tọa độ trong không gian thì \(A\left( {a,0,0} \right);B\left( {0,a\sqrt 2 ,0} \right);D\left( {a,a\sqrt 2 ,0} \right);C\left( {0,0,c} \right);M\left( {0,\frac{{a\sqrt 2 }}{2},\frac{c}{2}} \right)\)
Véc tơ chỉ phương \(\overrightarrow \alpha \left( {u,v,{\rm{w}}} \right) \ne 0\) của giao tuyến $(P)$ với $(OCD)$ phải thỏa mãn:
\(\overrightarrow \alpha ,\overrightarrow {OC} ,\overrightarrow {OD}\) đồng phẳng, tức là \(\overrightarrow \alpha = s.\overrightarrow {OC} + t.\overrightarrow {OD} = \left( {ta,ta\sqrt 2 ,sa} \right){\rm{ }}\left( {s,t \in R} \right)\)
\(\overrightarrow \alpha .\overrightarrow {AM} = 0\) mà \(\overrightarrow {AM} \left( { - a,\frac{{a\sqrt 2 }}{2},\frac{c}{2}} \right) \Rightarrow - t{a^2} + ta\sqrt 2 .\frac{{a\sqrt 2 }}{2} + s\frac{{ac}}{2} = s\frac{{ac}}{2} = 0\)
Vậy $s = 0$ và ta có thể coi \(\overrightarrow \alpha = \overrightarrow {OD} = \left( {a,a\sqrt 2 ,0} \right)\)
Mặt phẳng $(P)$ qua $A(a, 0 , 0)$ với $2$ véc tơ chỉ phương \(\overrightarrow {AM} ;\overrightarrow \alpha \) nên có véc tơ pháp tuyến
\(\overrightarrow n \left( {x,y,z} \right) \ne 0\) mà\(\left\{ \begin{array}{l}
- {\rm{ax}} + \frac{{a\sqrt 2 }}{2}y + \frac{c}{2}z\\
{\rm{ax}} + a\sqrt 2 y = 0
\end{array} \right. = 0\)
Vậy có thể chọn \(\overrightarrow y \left( {c\sqrt 2 , - c,3a\sqrt 2 } \right)\)
Từ đó $(P)$ có phương trình \(c\sqrt 2 \left( {x - a} \right) - cy + 3\sqrt 2 z = 0\)
$(P)$ cắt trục $Oz$ tại $E(0, 0, z)$ mà \( - ac\sqrt 2 + 3a\sqrt 2 z = 0 \Leftrightarrow E\left( {0,0,\frac{c}{3}} \right);OE = \frac{c}{3}\)
$2$. Vì \(\overrightarrow {OE} = \frac{1}{3}\overrightarrow {OC}\), giao tuyến $EF$ của $(P)$ với $(OCD)$ song song với $OD$ ($F $ thuộc $CD$) nên\(\overrightarrow {DF} = \frac{1}{3}\overrightarrow {DC}\)
Ta có tỉ số thể tích:
\(\frac{{{V_{CAEF}}}}{{{V_{CAOD}}}} = \frac{{CE}}{{CO}}.\frac{{CF}}{{CD}} = \frac{2}{3}.\frac{2}{3} = \frac{4}{9}\)
\(\frac{{{V_{CMEF}}}}{{{V_{CBOD}}}} = \frac{{CM}}{{CB}}.\frac{{CE}}{{CO}}.\frac{{CF}}{{CD}} = \frac{1}{2}.\frac{2}{3}.\frac{2}{3} =
\frac{2}{9}\)
Vậy \({V_{CAEMF}} = \left( {\frac{4}{9} + \frac{2}{9}} \right).\frac{1}{2}{V_{CAOBD}} = \frac{1}{3}{V_{CAOBD}}\)
Từ đó tỉ số thể tích hai khối đa diện được tạo thành khi cắt khối chóp $CAOBD$ bởi mặt phẳng $(P)$ là $\frac{1}{2}$ ( hay $2$)
$3$. Khoảng cách từ $C (0, 0, c)$ đến mặt phẳng $(P)$ là:
\(\frac{{\left| { - ac\sqrt 2 + 3a\sqrt 2 c} \right|}}{{\sqrt {2{c^2} + {c^2} + 18{a^2}} }} = \frac{{2ac\sqrt 6 }}{{2\sqrt {{c^2} + 6{a^2}} }}\)
|
|
|
Đăng bài 25-04-12 11:57 AM
|
|