|
|
1. Thế nào là thể tích của một khối đa diện
Một số tính chất về thể tích:
1) Hai khối đa diện bằng nhau thì có thể tích bằng nhau
2) Nếu 1 khối đa diện được phân chia thành các khối đa diện nhỏ thì thể tích của nó bằng tổng thể tích của các khối đa diện nhỏ
3) Khối lập phương có cạnh bằng 1 thì có thể tích bằng 1
2. Thể tích của khối hộp chữ nhật
Giả sử có 1 khối hộp chữ nhật với 3 kích thước a, b, c đều là những số dương. Khi đó thể tích của nó là:
$V = abc $
Ta có định lý:
- Định lý 1: Thể tích một khối hộp chữ nhật bằng tích của 3 kích thước
Ví dụ:
Tính thể tích của khối lập phương có các đỉnh là trọng tâm các mặt của 1 khối tám mặt đều cạnh a
Giải:

Giả sử có khối tám mặt đều với các đỉnh S, S’, A, B, C, D. Gọi M, N lần lượt là trọng tâm của tam giác SAB và tam giác SBC thì đoạn thẳng MN là 1 cạnh của khối lập phương. Gọi M’, N’ lần lượt là trung điểm của AB và BC thì M, N lần lượt nằm trên SM’, SN’ nên
$MN = \frac{2}{3}M'N' = \frac{2}{3}.\frac{{AC}}{2} = \frac{{a\sqrt 2 }}{3} $
Vậy thể tích của khối lập phương là:
$V = M{N^3} = \frac{{2{a^3}\sqrt 2 }}{{27}} $
3. Thế tích khối chóp
- Định lý 2: Thể tích của 1 khối chóp bắng một phần ba tích số của mặt đáy và chiều cao khối chóp đó
$V = \frac{1}{3}{S_{day}}.h $
Ví dụ:
Tính thể tích của khối tứ diện đều có cạnh bằng a
Giải:

- Xem tứ diện đều ABCD cạnh a như hình chóp có đỉnh A và đáy là tam giác đều BCD. Diện tích mặt đáy là:
${S_{BCD}} = \frac{{\sqrt 3 }}{4}{a^2} $
Gọi AH là chiều cao của hình chóp A.BCD thì H là tâm của tam giác đều BCD. Suy ra chiều cao hình chóp là: $h = AH = \sqrt {A{B^2} - B{H^2}} = \sqrt {{a^2} - \frac{{{a^2}}}{3}} = a\frac{{\sqrt 2 }}{{\sqrt 3 }} $
Từ đó suy ra khối tứ diện ABCD có thể tích là: $V = \frac{1}{3}{S_{BCD}}.h = \frac{{{a^3}\sqrt 2 }}{{12}} $
4. Thể tích của khối lăng trụ
- Định lý: Thể tích của khối lăng trụ bằng tích số của diện tích mặt đáy với chiều cao của khối lăng trụ đó
Ví dụ:
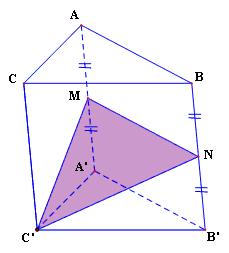
Cho khối lăng trụ ABC.A’B’C’. Gọi M, N lần lượt là trung điểm 2 cạnh AA’ và BB’. Mặt phẳng (MNC’) chia khối lăng trụ đã cho thành 2 phần. Tính tỉ số thể tích của 2 phần đó
Giải:
Nếu gọi V là thể tích khối lăng trụ thì thể tích khối tứ diện C’ABC là $\frac{V}{3} $.
Do đó thể tích của khối chóp C’.ABB’A là $\frac{{2V}}{3} $. Vì 2 khối chóp C’.ABNM và C’.MNB’A’ có cùng chiều cao và mặt đáy bằng nhau nên thể tích khối chóp C’.MNB’A’ là: $\overrightarrow {MA} .\overrightarrow {MB} = \overrightarrow 0 \Leftrightarrow MI = IA = IB $
và thể tích khối tứ diện ABCMNC’ là: ${V_2} = V - \frac{V}{3} = \frac{{2V}}{3} $
Ta có thể tích 2 phần được phân chia là: $k = \frac{{{V_1}}}{{{V_2}}} = \frac{1}{2} $
|