|
|
Phương tích
Cho đường tròn (O;R) và điểm M cố định. Một đường thẳng thay đổi đi qua M, cắt đường tròn đó tại 2 điểm A và B.
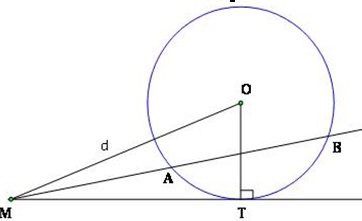
Khi đó, giá trị không đổi $\overrightarrow {MA} .\overrightarrow {MB} = {d^2} - {R^2}\,\,\,\,\,\,\,\,\,\,\,\,\,(d = MO)$ gọi là phương tích của điểm M đối với đường tròn (O) và kí hiệu là ${(P)_{M/(O)}}$
${(P)_{M/(O)}} = \overrightarrow {MA} .\overrightarrow {MB} = {d^2} - {R^2}\,\,\,\,\,\,\,\,(d = MO)$
* Khi điểm M nằm ngoài đường tròn (O), MT là tiếp tuyến của đường tròn đó ( T là tiếp điểm) thì
${(P)_{M/(O)}} = {\overrightarrow {MT} ^2} = M{T^2}$
|