|
|
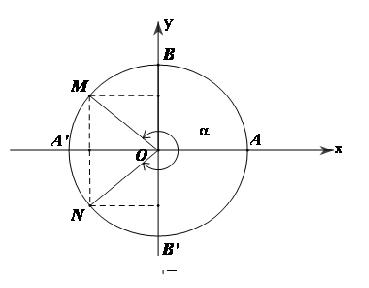
1. Hai góc đối nhau
$\left( {OA,OM} \right) = \alpha ,\left( {OA,ON} \right) = - \alpha $
$\begin{gathered}
\sin ( - \alpha ) = - \sin \alpha \\
c{\text{os}}( - \alpha ) = c{\text{os}}\alpha \\
\tan ( - \alpha ) = - \tan \alpha \\
\cot ( - \alpha ) = - \cot \alpha \\
\end{gathered} $
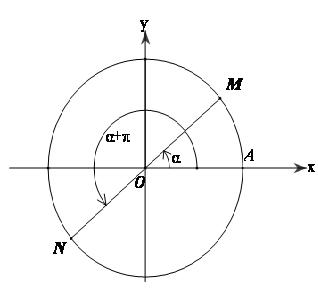
2. Hai góc hơn kém nhau $\pi $
$\left( {OA,OM} \right) = \alpha ,\left( {OA,ON} \right) = \alpha + \pi $
$\begin{gathered}
\sin (\alpha + \pi ) = - \sin \alpha \\
c{\text{os}}(\alpha + \pi ) = - c{\text{os}}\alpha \\
\tan (\alpha + \pi ) = \tan \alpha \\
\cot (\alpha + \pi ) = \cot \alpha \\
\end{gathered} $
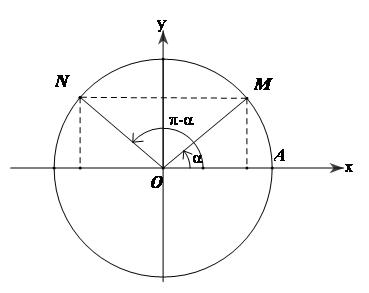
3. Hai góc bù nhau
$\left( {OA,OM} \right) = \alpha ,\left( {OA,ON} \right) = \pi - \alpha $
$\begin{gathered}
\sin (\pi - \alpha ) = \sin \alpha \\
c{\text{os}}(\pi - \alpha ) = - c{\text{os}}\alpha \\
\tan (\pi - \alpha ) = - \tan \alpha \\
\cot (\pi - \alpha ) = - \cot \alpha \\
\end{gathered} $
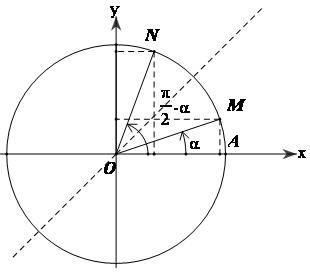
4. Hai góc phụ nhau
$\left( {OA,OM} \right) = \alpha ,\left( {OA,ON} \right) = \frac{\pi }{2} - \alpha $
$\begin{gathered}
\sin (\frac{\pi }{2} - \alpha ) = c{\text{os}}\alpha \\
c{\text{os}}(\frac{\pi }{2} - \alpha ) = {\text{sin}}\alpha \\
\tan (\frac{\pi }{2} - \alpha ) = \cot \alpha \\
\cot (\frac{\pi }{2} - \alpha ) = \tan \alpha \\
\end{gathered} $
Nhận xét
Nhờ các công thức trên, ta có thể đưa việc tính giá trị lượng giác của một góc lượng giác tùy ý về việc tính giá trị lượng giác của góc$\alpha $, $0 \leqslant \alpha \leqslant \frac{\pi }{2}$ , thậm chí $0 \leqslant \alpha \leqslant \frac{\pi }{4}$.
CHÚ Ý
Nếu số đo của góc hình học uOv là $\alpha $($0 \leqslant \alpha \leqslant \pi $) thì số đo của góc lượng giác tùy ý (Ou, Ov) bằng $\alpha + k2\pi $hoặc $ - \alpha + k2\pi (k \in \mathbb{Z})$. Do đó, từ các công thức $c{\text{os}}( - \alpha ) = c{\text{os}}\alpha \,\,;\,\,\sin ( - \alpha ) = - \sin \alpha $ ta có
Với một góc lượng giác (Ou, Ov) tùy ý.
|