|
|
Giả sử ΔABC nội tiếp (O,R), I là trung điểm cung BC chứa điểm A và đặt ^BAC=α.
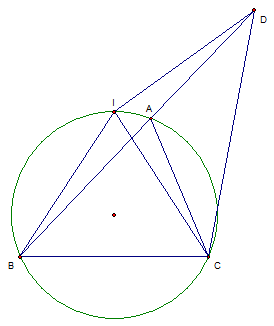
Trên tia đối của tia AB đựng điểm D sao cho AD=AC. Khi đó ^BDC=α2=12^BIC, suy ra D∈(I,IB).
Ta suy ra: AB+AC=BD≤2BI. Khi đó:
SABC=12AB.ACsinα≤12BI2sinα=2R2cos2α2sinα=4R2cos3α2sinα2.
Ta có cos3α2sinα2≤3√316. Dấu = xảy ra khi và chỉ khi α=600.
Tóm lại ΔABC đạt diện tích lớn nhất khi và chỉ khi ΔABC đều.
|