Ta biến đổi vế trái của đẳng thức:
$VT=\frac{1}{\sin^2\alpha }.\frac{1}{\cos^2\alpha }=(1+\cos^2\alpha )(1+\tan^2\alpha )  \\  = 1 + {\tan ^2}\alpha  + {\cot ^2}\alpha  + {\tan ^2}\alpha .{\cot ^2}\alpha  = 1 + {\tan ^2}\alpha  + {\cot ^2}\alpha  + 1\\  = {\tan ^2}\alpha  + {\cot ^2}\alpha  + 2  (đpcm)$

$\int\limits_{\frac{\pi }{6}}^{\frac{\pi }{3}} {\sqrt {(\tan^2x + \cot ^2x - 2)} \,dx}$
$=\int\limits_{\frac{\pi}{6} }^{\frac{\pi}{3} } \sqrt{(\tan x-\cot x)^2}  dx=\int\limits_{\frac{\pi}{6} }^{\frac{\pi}{3} }  |\tan x-\cot x|dx$
$=\int\limits_{\frac{\pi}{6} }^{\frac{\pi}{3} }|\frac{2\cos2x}{\sin2x} |dx=\int\limits_{\frac{\pi}{6} }^{\frac{\pi}{4} }\frac{2\cos2x}{\sin2x}dx-\int\limits_{\frac{\pi}{4} }^{\frac{\pi}{3} } \frac{2\cos2x}{\sin2x}dx$
$=\int\limits_{\frac{\pi}{6} }^{\frac{\pi}{4} }\frac{d\sin2x}{\sin2x}-\int\limits_{\frac{\pi}{4} }^{\frac{\pi}{3} } \frac{d\sin2x}{\sin2x}$
Đặt $t=\sin2x$ thì
$I=\int\limits_{\frac{\sqrt{3} }{2} }^{1} \frac{dt}{t}-\int\limits_{1}^{\frac{\sqrt{3} }{2} }\frac{dt}{t}   =2\int\limits_{\frac{\sqrt{3} }{2} }^{1}\frac{dt}{t} =2lnt\mathop |\nolimits_\frac{\sqrt{3} }{2} ^1  =2ln\frac{2}{\sqrt{3} }$

Điều kiện : $x>0$.
Đặt $t=log_6x\Leftrightarrow  x=6^t$ thế thì:
$x^{log_6(3x)}=6^{t(log_63+t)}$ và $36\sqrt[5]{x^7} =6^2.6^{\frac{7t}{5} }=6^{2+\frac{7t}{5} }$
Thay vào PT ta được :
$6^{t(log_63+t)}=6^{2+\frac{7t}{5} }\Leftrightarrow  t(log_63+t)=2+\frac{7t}{5} \Leftrightarrow  5t^2-(7-5log_63)t-10=0$
Phương trình có các hệ số $a,c$ trái dấu nên luôn có hai nghiệm phân biệt $t_1,t_2$ thỏa mãn $t_1+t_2=\frac{7-5log_63}{5}$
Mặt khác ta có $x_1=6^{t_1}, x_2=6^{t_2}$ nên
$x_1.x_2=6^{t_1+t_2}=6^{\frac{7-5log_63}{5} }=2\sqrt[5]{36}$

Hệ $\begin{cases}x+y+a=1                  (1)\\ 2^{a^2}.4^{x+y-xy}=2        (2) \end{cases}$
$(1) \Leftrightarrow  x+y=1-a$
$(2)\Leftrightarrow  2^{2(x+y-xy)}=2^{1-a^2}$
$\Leftrightarrow  2(x+y-xy)=1-a^2$
$\Leftrightarrow  x+y-xy=\frac{1-a^2}{2}$
$\Leftrightarrow  xy=1-a-\frac{1-a^2}{2}=\frac{a^2-2a+1}{2}$
Hệ$\Leftrightarrow  \begin{cases}x+y=1-a \\ xy=\frac{(1-a)^2}{2}  \end{cases}$
$\Leftrightarrow  x,y$  là hai nghiệm của phương trình
$t^2-(1-a)t+\frac{(1-a)^2}{2} =0              (3)$
$(3)$ có $\Delta =(1-a)^2-2(1-a)^2=-(1-a)^2$
Do đó : - Nếu $a\neq  1$ thì $\Delta <0,(3)$ nghiệm
$\Rightarrow$ Hệ  vô nghiệm.
- Nếu $a=1$ thì $(3)\Leftrightarrow  t^2=0\Leftrightarrow  t=0$
Hệ  có nghiệm duy nhất $x=y=0$

Lời giải này có yêu cầu trả vỏ sò để xem. Bạn hãy link trên để vào xem chi tiết

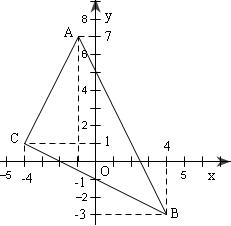
$1.$ Dễ tính độ dài các cạnh tam giác $ABC$ là:
$AB = 5\sqrt 5 ;AC = 3\sqrt 5 ;BC = 4\sqrt 5$
Đường phân giác trong góc $A$ có phương trình dạng:
$a(x + 1) + b(y-7) = 0$ sao cho $2$ điểm $(4;-3) và C(-4;1)$ ở $2$ phía của nó và tỉ số khoảng cách từ $B$ và $C$ đến nó tỉ lệ với $\frac{{BA}}{{CA}} = \frac{5}{3}$, tức là:
$\frac{{a(4 + 1) + b( - 3 - 7)}}{{a( - 4 + 1) + b(1 - 7)}} =  - \frac{5}{3} \Leftrightarrow \frac{{a - 2b}}{{a + 2b}} = 1$
Vậy $b = 0;a \ne 0$
Từ đó đường phân giác có phương trình: $x + 1 = 0$
Đường phân giác trong $C$ có phương trình dạng: $\alpha (x + 4) + \beta (y - 1) = 0$sao cho $2$ điểm $A(-1;7) ; B(4;-3)$ ở  $2$ phía của nó và tỉ số khoảng cách từ $A$ và $B$ đến nó tỉ lệ với $\frac{{AC}}{{BC}} = \frac{3}{4}$ tức là:
$\frac{{\alpha ( - 1 + 4) + \beta (y - 1)}}{{\alpha (4 + 4) + \beta ( - 3 - 1)}} =- \frac{3}{4}$ tức là: $\frac{{\alpha  + 2\beta }}{{2\alpha  - \beta }} = - 1$
Lấy $\alpha  = 1;\beta  =  - 3$và được pt đường phân giác đó là $x – 3y + 7 = 0.$
Giao điểm $I$ của $2$ phân giác đó là $I(-1;2).$ Viết phương trình đường thẳng $AB$, có $2x + 5y – 5 = 0$
Khoảng cách từ I đến đường thẳng này là $\sqrt 5$=> pt đường tròn nội tiếp là:
${(x + 1)^2} + {(y - 2)^2} = 5$
$2.$ Pt chùm mặt phẳng trục ($a$) là:
$\begin{array}{l} \alpha (2x + 3y - 1) + \beta (y + z + 1) = 0\\  \Leftrightarrow 2\alpha x + (3\alpha  + \beta )y + \beta z - \alpha  + \beta  = 0\,\,\,(1) \end{array}$
Mp ($1$) sẽ song song với ($b$)
$\begin{array}{l}  \Leftrightarrow (2\alpha ;3\alpha  + \beta ;\beta )(3;2;0) = 0\\  \Leftrightarrow \beta  =  - 6\alpha \end{array}$
Thế vào ($1$) ta được :
$\begin{array}{l} 2\alpha x - 3\alpha y = 6\alpha z - 7\alpha \\  \Leftrightarrow 2x - 3y - 6z - 7 = 0\,\,\,(1') \end{array}$
Đường thẳng ($b$) chứa điểm $B(-1 ;2 ;1). B$ cách mặt phẳng ($1’$) một khoảng là :
$\frac{{| - 2 - 6 - 6 - 7|}}{{\sqrt {{2^2} + {3^2} + {6^2}} }} = 3$
Vậy $a, b$ cách nhau một khoảng bẳng $3.$

1) $k \in {N^ + }$. Với $k = 1$ ta có
    $f({x^1}) = 1.{x^o}f(x) = 1.{x^{1 - 1}}f(x)$    : (2) đúng
Giả sử (2) đúng với $k = n \in {N^ + }$:
    $f({x^n}) = n{x^{n - 1}}f(x)$            (*)
Theo nguyên lý nạp toán học ta cần chứng minh (2) đúng với $k = n + 1$. Theo (1) ta có
    $\begin{array}{l} f({x^{n + 1}}) = f({x^n}x) = {x^n}f(x) + xf({x^n})  = {x^n}f(x) + x.n{x^{n - 1}}f(x){\rm{  (do (*))}} {\rm{ = (n + 1)}}{{\rm{x}}^n}f(x) \end{array}$
2) $k \in Q,k > 0$, tức là $k = \frac{p}{q}$ trong đó $p,q \in {N^ + }$. Theo chứng minh phần 1) ta có
    $\begin{array}{l} f({x^p}) = p{x^{p - 1}}f(x),\\ f[{({x^{p/q}})^q}{\rm{]}} = q{({x^{p/q}})^{q - 1}}f({x^{p/q}})\\ \Leftrightarrow f({x^{p/q}}) = \frac{p}{q}{x^{p/q - 1}}f(x) \end{array}$
Tức là $f({x^k}) = k{x^{k - 1}}f(x)$
3) $k \in R,k > 0$. Khi đó ta chọn được dãy số hữu tỉ dương     ${k_1},{k_2}....$ để  $\mathop {\lim }\limits_{n \to \infty } {k_n} = k$
Theo giả thiết, f(x) liên tục nên đối với mọi     $x > 1$ ta có
$f({x^k}) = \mathop {\lim }\limits_{n \to \infty } f({x^{{k_n}}}) = \mathop {\lim }\limits_{n \to \infty } {k_n}{x^{{k_n} - 1}}f(x)$    (do (2))
            $= k.{x^{k - 1}}f(x).$

a) Ta có: $\overrightarrow{AB}=(1;3)$ và $\overrightarrow{AC}=(9;-3)$
Nên $\overrightarrow{AB}.\overrightarrow{AC}=9-9=0$. Vậy tam giác $ABC$ vuông ở $A$.
b) $\overrightarrow{BA}=(-1;-3),\overrightarrow{BC}=(8;-6)$
Do đó $\overrightarrow{BA}.\overrightarrow{BC}=-8+18=10,\overrightarrow{BA}=\sqrt{1^2+3^2}=\sqrt{10}$
$\overrightarrow{BC}=\sqrt{8^2+6^2}=10$, mà $\overrightarrow{BA}.\overrightarrow{BC}=BA.BC.\cos B$
$\Rightarrow 10=\sqrt{10}\cos B$. Vậy $\cos B=\frac{1}{\sqrt{10}}$
Tương tự ta có: $\overrightarrow{CA}.\overrightarrow{CB}=90 \Rightarrow \cos C=\frac{3}{\sqrt{10}}$

Lời giải này có yêu cầu trả vỏ sò để xem. Bạn hãy link trên để vào xem chi tiết

a) Ta có:  $\sin (810^0+x)=\sin (90^0+x)=\cos x$
   $\cos (1260^0-x)=\cos (180^0-x)=-\cos x$
   $\tan (630^0+x)=\tan (90^0+x)=-\cot x$
   $\tan (1260^0-x)=\tan (180^0-x)=-\tan x$
Do đó:  $A=2\cos x -\cos x +(-\cot x )(-\tan x )   \Rightarrow    A=1+\cos x$
Vì  $-1 \leq \cos x \leq 1$  với mọi  $x$  , ta suy ra  $A\geq 0$  với mọi $x$.
b) Với  $x=1935^0  \Rightarrow    A=1+\cos 1935^0   \Rightarrow    A=1+\cos 135^0$
$A=1-\cos 45^0   \Rightarrow    A=1-\frac{\sqrt{2} }{2}$

Trọng tâm $G$ có tọa độ:
$x_G=\frac{x_A+x_B+x_C}{3}=\frac{2}{3},y_G=\frac{y_A+y_B+y_C}{3}=2$. Vậy $G(\frac{2}{3};2)$
Gọi $H(x;y)$ là trực tâm ta có:
$\left\{ \begin{array}{l} \overrightarrow{AH}.\overrightarrow{BC}=0\\\overrightarrow{BH}.\overrightarrow{CA}=0  \end{array} \right.  \Leftrightarrow  \left\{ \begin{array}{l} (x+3)(2-3)+(y-0)(6-0)=0\\(x-3)(-3-2)+(y-0)(0-6)=0 \end{array} \right.$
$\Leftrightarrow  \left\{ \begin{array}{l} -x+6y=3\\ -5x-6y=-15 \end{array} \right.  \Leftrightarrow \left\{ \begin{array}{l} x=2\\ y=\frac{5}{6}  \end{array} \right.$. Vậy $H(2;\frac{5}{6})$

Gọi $I(x,y)$ là tâm đường tròn ngoại tiếp tam giác, ta có:
$IA=IB=IC  \Leftrightarrow  \left\{ \begin{array}{l} IA^2=IB^2\\ IA^2=IC^2 \end{array} \right.  \Leftrightarrow  \left\{ \begin{array}{l} (x-4)^2+(y-6)^2=(x-5)^2+(y-1)^2\\ (x-4)^2+(y-6)^2=(x-1)^2+(y+3)^2 \end{array} \right.$
$\Leftrightarrow  \left\{ \begin{array}{l} 2x-10y=-26\\ -6x-18y=-42 \end{array} \right.  \Leftrightarrow  \left\{ \begin{array}{l} x=-\frac{1}{2} \\ y =\frac{5}{2} \end{array} \right.$
Vậy tâm $I \left (-\frac{1}{2};\frac{5}{2} \right)$ và bán kính $IA=\sqrt{\left (-\frac{1}{2}-4\right)^2+\left (\frac{5}{2}-6\right)^2}=\frac{\sqrt{130}}{2}$

Ta có : $DC//AB\Rightarrow  DC//(SAB)$
$\Rightarrow  mp(MDC)\cap mp(SAB)=MN//AB$.Lại có $MN\bot (SAD)$.Suy ra tứ giác $MNCD$ là hình thang vuông.
Diện tích $MNCD$ là :
$S_{MNCD}=\frac{1}{2} (MN+CD)MD$
Trong đó : $CD=a$
$MD=\sqrt{MA^2+AD^2} =\sqrt{x^2+a^2}$
Trong $\Delta SAB$ ta có $MN//AB$ suy ra
$\frac{MN}{AB}=\frac{SM}{SA}\Rightarrow  \frac{MN}{a}   =\frac{a-x}{a} \Rightarrow  MN=a-x$
Do đó $S_{MNCD}=\frac{1}{2}\sqrt{x^2+a^2}.(a+a-x)=\frac{1}{2}   \sqrt{x^2+a^2}(2a-x)$

Chọn hệ trục tọa độ $Axyz$ sao cho: $A(0;0;0), B(a;0;0), C(a;a;0), D(0;a;0), S(0;0;h)$
$M(a;a-x;0), N(a-y;a;0), 0<x,y<a$
a) Ta có: $\left\{ \begin{array}{l} AS\bot AM\\ AS\bot AN \end{array} \right. (do  AS\bot (ABCD))$
$\Rightarrow  [M,AS,N]=(\overrightarrow{AM},\overrightarrow{AN}  )$
$\overrightarrow{AM}=(a;a-x;0), \overrightarrow{AN}=(a-y;a;0)$
$cos 45^0=\frac{\overrightarrow{AM},\overrightarrow{AN}  }{|\overrightarrow{AM} |.|\overrightarrow{AN} |} =\frac{a(a-y)+(a-x)a}{\sqrt{(2a^2-2ax+x^2)(2a^2-2ay+y^2)} }$
$\Leftrightarrow  2a^2(4a^2+x^2+y^2-4ax-4ay+2xy)=(2a^2-2ax+X^2)(2a^2-2ay+y^2)$
Vậy hệ thức là $4a^2-4a^3(x+y)+2axy(x+y)-x^2y^2=0$
b) Tìm $x,y$ để $(SAM)\bot (SMN)$
Ta có: $\left\{ \begin{array}{l} (SAM)\bot (AMN)\\ (SAM)\bot (SMN) \end{array} \right. \Rightarrow  MN\bot (SAM)$
$\Rightarrow$ để $(SAM)\bot (SMN)$ thì $AM\bot MN$
$\Rightarrow  \overrightarrow{AM}.\overrightarrow{MN}=0\Rightarrow  (a;a-x;0)(-y;x;0)=0\Leftrightarrow  x^2-ax+ay=0$
Vậy hệ thức là $x^2-ax+ay=0$

$a.$ Ta đi chứng minh bằng phản chứng.Thât vậy giả sử $OA,MN$  không chéo nhau tức chúng nằm trong một mặt phẳng.Mặt phẳng này chứa ba điểm $A,M,N$ không thẳng hàng, đó chính là mặt phẳng $\alpha$ suy ra :
$O\in \alpha$ trái với giả thiết
Vậy $OA,MN$ chéo nhau
$b.$ Gọi $C$ là trung điểm $AB$ nhận xét rằng :
$ABNM$ là hình thang
$\Rightarrow  I\in Cz$ là đường trung bình của $ABNM$- cố định
Vậy $OI$ nằm trong mặt phẳng cố định $(O;Cz)$
$c.$ Xét hình thang $ABNM$ ta có :
$CI=\frac{1}{2} (AM+BN)$- không đổi $\Rightarrow  I cố đinh$
Vậy mặt phẳng $(OMN)$ chứa đường thẳng $OI$ cố định