|
|
giải đáp
|
mk là mem ms mong mn giúp đỡ...
|
|
|
|
Cách khác: Dùng đạo hàm $y'=1-\frac{11}{2x^2}-\frac{14}{x^3\sqrt{1+\frac{7}{x^2}}}=\frac{2x^2\sqrt{x^2+7}-11\sqrt{x^2+7}-28}{2x^2\sqrt{x^2+7}}$ $y'=0$ => $2x^2\sqrt{x^2+7}-11\sqrt{x^2+7}-28=0$ Đặt $t=\sqrt{x^2+7}$ ($t>\sqrt{7}$) => $x^2=t^2-7$ => $2(t^2-7)t-11t-28=0$ => $2t^3-25t-28=0$ => $t=4$ => $x=3$ Xét bảng biến thiên => $Miny=\frac{15}{2}$ tại x=3 |
|
|
|
giải đáp
|
Dấu $"="$ xảy ra khi nào?
|
|
|
|
Ta có:
=SMAB+SMBC+SMCA⇔SMABSABC+SMBCSABC+SMCASABC=1⇔zhc+yhb+xha=1
⇒ha+hb+hc=(ha+hb+hc)(zhc+yhb+xha)
Theo Bunhiacốpxki thì:
x√+y√+z√=ha−−√x√ha−−√+hb−−√y√hb−−√+hc−−√z√hc−−√⩽(ha+hb+hc)(x√ha−−√+y√hb−−√+z√hc−−√)−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−⎷=ha+hb+hc−−−−−−−−−−√
mà S=12aha=12absinC⇒ha=bsinC, hb=csinA, hc=asinB
⇒ha+hb+hc−−−−−−−−−−√=(asinB+bsinC+csinA)−−−−−−−−−−−−−−−−−−−−−√=ab2R+bc2R+ca2R−−−−−−−−−−−−−√
⇒x√+y√+z√⩽ab2R+bc2R+ca2R−−−−−−−−−−−−−√⩽a2+b2+c22R−−−−−−−−−−√⇒ Đpcm.
Đẳng thức xảy ra khi và chỉ khi {=b=cx=y=z⇔ΔABCđều và M là tâm đường tròn nội tiếpΔABC.
|
|
|
|
đặt câu hỏi
|
BĐT số 7
|
|
|
|
Tìm giá trị nhỏ nhất của hàm số $y=x+\frac{11}{2x}+\sqrt{4(1+\frac{7}{x^2})}$ với $x>0$
|
|
|
|
giải đáp
|
10 vỏ sò khi làm hết
|
|
|
|
Lời giải này có yêu cầu trả vỏ sò để xem. Bạn hãy link trên để vào xem chi tiết
|
|
|
|
giải đáp
|
pt bậc cao...
|
|
|
|
Điều kiện ![x\in \left [ -1,1 \right ] x\in \left [ -1,1 \right ]](https://s0.wp.com/latex.php?latex=x%5Cin+%5Cleft+%5B+-1%2C1+%5Cright+%5D&bg=ffffff&fg=000&s=0) . Đặt . Đặt ![x=cost,\;\;t\in \left [ 0,\pi \right ] x=cost,\;\;t\in \left [ 0,\pi \right ]](https://s0.wp.com/latex.php?latex=x%3Dcost%2C%5C%3B%5C%3Bt%5Cin+%5Cleft+%5B+0%2C%5Cpi+%5Cright+%5D&bg=ffffff&fg=000&s=0) Khi đó phương trình trở thành : 
Với điều kiện ![t\in \left [ 0,\pi \right ],l,k\in \mathbb{Z} t\in \left [ 0,\pi \right ],l,k\in \mathbb{Z}](https://s0.wp.com/latex.php?latex=t%5Cin+%5Cleft+%5B+0%2C%5Cpi+%5Cright+%5D%2Cl%2Ck%5Cin+%5Cmathbb%7BZ%7D&bg=ffffff&fg=000&s=0) ta tìm được ta tìm được 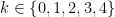 và và 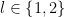 . . Suy ra 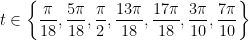 Thử lại ta kết luận được tập nghiệm của phương trình là  |
|
|
|
giải đáp
|
giúp em với !
|
|
|
|
Sau 1h ô tô đi đc 56.1=56 (km) => Quãng đường còn lại là: 287-56=231 (km) Gọi tgian từ lúc xe đạp đi đến lúc gặp ô tô là t (h) => Quãng đường ô tô đi đc là 56t (km) Quãng đường xe đạp đi đc là 10t (km)
Có: 56t+10t=231 => 66t=231 => t=3,5 h = 3h30' => Quãng đường ô tô đi đc là 196 (km) => vị trí ô tô khách và xe đạp gặp nhau cách A: 56+196=252
|
|
|
|
đặt câu hỏi
|
LG
|
|
|
|
$A=a(cos^8x-sin^8x)+4(sin^6x+cos^6x)+b.sin^4x$. tìm a, b để biểu thức không phụ thuộc vào biến Xem thêm : Mời mọi người tham gia cuộc thi do các Admin tổ chức nhé CLICK ! TOPIC về HỆ-BẤT-PHƯƠNG TRÌNH trong các đề thi Click ! |
|
|
|
đặt câu hỏi
|
Hpt
|
|
|
|
$\begin{cases}3x-y=\sqrt{7x^4-6x^2y^2+2x^3y+y^2} \\ \frac{xy+2}{2}+\frac{1}{x^2+y^2}=\frac{3x^2+2xy+3y^2}{(x^2+y^2)} \end{cases}$ $(x,y$ $\epsilon$ $ R)$Xem thêm : Mời mọi người tham gia cuộc thi do các Admin tổ chức nhé CLICK ! TOPIC về HỆ-BẤT-PHƯƠNG TRÌNH trong các đề thi Click ! |
|
|
|
giải đáp
|
phương trình đường tròn
|
|
|
|
a) AB có vtpt n(4;-1) => pt AB: $4(x-1)-y+3=0$ => $4x-y-1=0$ b) $(C): x^2-4x+4+y^2-2y+1-9=0$ <=> $(x-2)^2+(y-1)^2=9$ $(C1)$ có tâm $A(1;3)$, bk $R'=d(A;\Delta)$ => $R'=\frac{2.1-3+5}{\sqrt{2^2+1}}$ => $R'^2=\frac{16}{5}$ => $(C1): (x-1)^2+(y-3)^2=\frac{16}{5}$ |
|
|
|
đặt câu hỏi
|
Bài này có bao nhiêu cách???
|
|
|
|
Cho $x,y,z$ là 3 số dương và $x+y+z \le 1$. CMR: $\sqrt{x^2+\frac{1}{x^2}}+\sqrt{y^2+\frac{1}{y^2}}+\sqrt{z^2+\frac{1}{z^2}} \ge \sqrt{82}$ |
|
|
|
đặt câu hỏi
|
BĐT số 6
|
|
|
|
Cho các số thực dương $x, y, z$ thỏa mãn $\sqrt{3x^2+3y^2-4xy}+\sqrt{3y^2+3z^2-4yz}+\sqrt{3z^2+3x^2-4zx} \le 3\sqrt{2}$. Tìm min: $T=\frac{1}{\sqrt{8^x+1}}\frac{1}{\sqrt{8^y+1}}+\frac{1}{\sqrt{8^z+1}}$ |
|
|
|
đặt câu hỏi
|
BĐT số 5
|
|
|
|
Cho các số thực dương $x, y, z$ thỏa mãn $xyz=1$. CMR: $\frac{\sqrt{1+x^3+y^3}}{xy}+\frac{\sqrt{1+y^3+z^3}}{yz}+\frac{\sqrt{1+z^3+x^3}}{zx} \ge 3\sqrt{3}$ |
|
|
|
đặt câu hỏi
|
BĐT số 4
|
|
|
|
CMR với mọi số thực dương $x, y, z$ thỏa mãn $x(x+y+z)=3yz$, ta có: $(x+y)^3+(x+z)^3+3(x+y)(x+z)(y+z) \le 5(y+z)^3$ |
|
|
|
giải đáp
|
BĐT số 2
|
|
|
|
$P=\frac{3(x^2+y^2)+3(x+y)}{4}+\frac{3-(x+y)}{x+y}-(x^2+y^2)$ $=-\frac{x^2+y^2}{4}+\frac{3(x+y)}{4}+\frac{3}{x+y}-1$ $=-\frac{(x+y)^2}{4}+(x+y)-1-\frac{x+y}{4}+\frac{3}{x+y}+\frac{xy}{2}$ $=-(\frac{x+y}{2}-1)^2-\frac{x+y}{4}+\frac{3}{x+y}+\frac{3-(x+y)}{2}$ $=-(\frac{x+y}{2}-1)^2-3(\frac{x+y}{4}-\frac{1}{x+y})+\frac{3}{2}$ $=-(\frac{x+y}{2}-1)^2-3.\frac{(x+y)^2-4}{4(x+y)}+\frac{3}{2}$ (1) Ta có: $3=xy+x+y \le \frac{(x+y)^2}{4}+x+y=(\frac{x+y}{2}+1)^2-1$
=> $(\frac{x+y}{2}+1)^2 \ge 4$ => $x+y \ge 2$ => $(x+y)^2 \ge 4$ (do $x+y>0$) (2) từ (1) và (2) => $P \le \frac{3}{2}$ Dấu = xảy ra <=> $x=y=1$ Vậy $P_{max}=\frac{3}{2}$ tại $x=y=1$ |
|
|
|
đặt câu hỏi
|
BĐT số 3
|
|
|
|
Cho $x, y, z$ là ba số thực thuộc đoạn [$1;4$] và $x \ge y, y \ge z$. Tìm GTNN của $P=\frac{x}{2x+3y}+\frac{y}{y+z}+\frac{z}{z+x}$ |
|