|
|
1. Định nghĩa mặt cầu
- Định nghĩa: Tập hợp các điểm trong không gian cách điểm O cố định 1 khoảng R không đổi gọi là mặt cầu có tâm là O và bán kính bằng R
- Mặt cầu như thế thường được kí hiệu là S(O;R). Như vậy:
$S(O;R) = {\text{\{ }}M/OM = R{\text{\} }} $
- Các thuật ngữ:
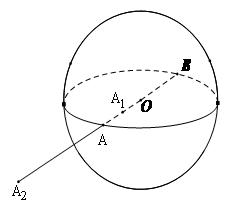
Cho mặt cầu S(O;R) và 1 điểm A nào đó
a) Nếu OA = R thì theo định nghĩa, điểm A thuộc mặt cầu. Khi đó đoạn thẳng OA cũng được gọi là bán kính của mặt cầu
Nếu OA và OB cùng là bán kính mặt cầu và 3 điểm A, O, B thẳng hàng thì đoạn thẳng AB được gọi là đường kính của mặt cầu. Như vậy một mặt cầu được xác định khi biết tâm và bán kính R hoặc khi biết 1 đường kính AB của nó
b) Nếu OA < R thì ta nói điểm A nằm trong mặt cầu
c) Nếu OA > R thì ta nói điểm A nằm ngoài mặt cầu
- Ví dụ: Cho 2 điểm A, B cố định. Chứng minh rằng tập hợp các điểm M sao cho $\overrightarrow {MA} .\overrightarrow {MB} = \overrightarrow 0 $ là mặt cầu đường kính AB
Giải: Gọi I là trung điểm AB. Ta có:
$\begin{gathered}
\overrightarrow {MA} .\overrightarrow {MB} = (\overrightarrow {MI} + \overrightarrow {IA} ).(\overrightarrow {MI} + \overrightarrow {IB} ) \\
\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = (\overrightarrow {MI} + \overrightarrow {IA} ).(\overrightarrow {MI} - \overrightarrow {IA} ) = M{I^2} - I{A^2} \\
\end{gathered} $
Suy ra $\overrightarrow {MA} .\overrightarrow {MB} = \overrightarrow 0 \Leftrightarrow MI = IA = IB $
Vậy tập hợp các điểm M là mặt cầu tâm I bán kính R = IA tức là mặt cầu đường kính AB
2. Vị trí tương đối giữa mặt cầu và mặt phẳng
HV 33/40
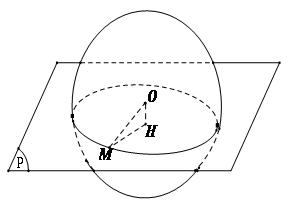
Cho mặt cầu S(O;R) và mặt phẳng (P). .Gọi H là hình chiếu của O trên mặt phẳng (P) thì d = OH. Khi đó:
- Nếu d < R thì thì mp(P) cắt mặt cầu S(O:R) theo giao tuyến là đường tròn nằm trên mp(P) có tâm là H và bán kính
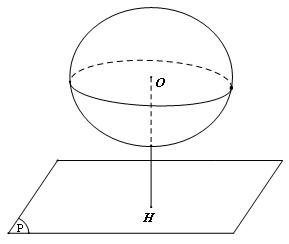
- Nếu d = R thì mp(P) cắt mặt cầu tại 1 điểm duy nhất H
- Nếu d > R thì mp(P) không cắt mặt cầu S(O;R)
Khi d = 0 thì mp(P) đi qua tâm O của mặt cầu, mặt phẳng đó được gọi là mặt phẳng kính, giao tuyến của mặt phẳng kính với mặt cầu là đường tròn có bán kính R gọi là đường tròn lớn của mặt cầu
Khi d = R thì mp(P) và mặt cầu S(O;R) có điểm chung duy nhất là H. Khi đó ta nói mặt phẳng (P) tiếp xúc với mặt cầu S(O;R) tại điểm H hoặc còn nói mp(P) là tiếp diện của mặt cầu tại điểm H, điểm H gọi là điểm tiếp xúc ( hoặc tiếp điểm ) của (P) và mặt cầu
3. Vị trí tương đối giữa mặt cầu và đường thẳng
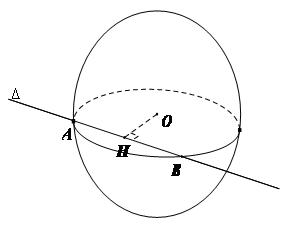
Cho mặt cầu S(O;R) và đường thẳng $\Delta $. Gọi H là hình chiếu của O trên $\Delta $ và d = OH là khoảng cách từ O tới $\Delta $. Ta có:
- Nếu d < R thì $\Delta $ cắt mặt cầu tại 2 điểm phần biệt
- Nếu d = R thì $\Delta $ cắt mặt cầu tại 1 điểm duy nhất
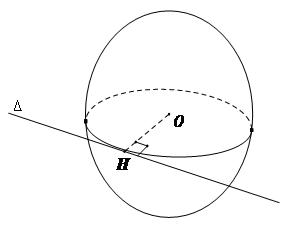
- Nếu d > R thì $\Delta $ không cắt mặt cầu
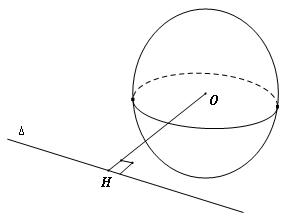
Trong trường hợp d = R người ta nói đường thẳng $\Delta $ và mặt cầu S(O;R) có điểm chung duy nhất là H. Khi đó đường thẳng $\Delta $ tiếp xúc với mặt cầu tại điểm H hay còn gọi $\Delta $ là tiếp tuyến của mặt cầu, điểm H gọi là tiếp điểm của $\Delta $ và mặt cầu.
Định lý: Nếu 1 điểm A nằm ngoài mặt cầu S(O;R) thì:
a) Qua A có vô số tiếp tuyến với mặt cầu
b) Độ dài các đoạn thẳng nối A với các tiếp điểm bằng nhau
c) Tập hợp các tiếp điểm là 1 đường tròn nằm trên mặt cầu
4. Diện tích mặt cầu và thể tích khối cầu
Ta có các công thức sau:
- Mặt cầu bán kính R có diện tích là: $S = 4.\pi .{R^2} $
- Khối cầu bán kính R có thể tích là : $V = \frac{4}{3}.\pi .{R^3} $
|