|
|
1. Định nghĩa tích của một vectơ với một số
ĐỊNH NGHĨA
Tích của vectơ $\overrightarrow a $ với số thực k là một vectơ, kí hiệu là $k\overrightarrow a $ được xác định như sau
1) Nếu $k \geqslant 0$ thì vectơ $k\overrightarrow a $cùng hướng với vectơ $\overrightarrow a $
Nếu $k < 0$ thì vectơ $k\overrightarrow a $ ngược hướng với vectơ $\overrightarrow a $
2) Độ dài của vectơ $k\overrightarrow a $ bằng $\left| k \right|.\,\left| {\overrightarrow a } \right|$
Phép lấy tích của vectơ với một số gọi là phép nhân vectơ với số (hoặc phép nhân số với vectơ)
Nhận xét:
Từ định nghĩa ta thấy ngay $1\overrightarrow a = \overrightarrow a ,\,\,( - 1)\overrightarrow a $ là vectơ đối của $\overrightarrow a $, tức là $( - 1)\overrightarrow a = - \overrightarrow a $
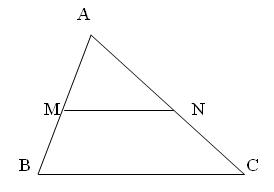
Vi dụ : Ta có tam giác $ABC$ với $M$ và $N$ lần lượt là trung điểm hai cạnh $AB$ và $AC$. Khi đó ta có:
a) $\overrightarrow {BC} \, = 2\,\overrightarrow {MN} ;\,\,\,\overrightarrow {MN} \, = \frac{1}{2}\,\overrightarrow {BC} $
b)$\overrightarrow {BC} \, = \left( { - 2} \right)\,\overrightarrow {NM} ;\,\,\,\overrightarrow {MN} \, = \left( { - \frac{1}{2}} \right)\,\overrightarrow {CB} $
c)$\overrightarrow {AB} \, = 2\,\overrightarrow {MB} ;\,\,\,\overrightarrow {AN} \, = \left( { - \frac{1}{2}} \right)\,\overrightarrow {CA} $
2. Các tính chất của phép nhân vectơ với số
Với hai vectơ bất kì $\overrightarrow a $, $\overrightarrow b $ và mọi số thực $k, l$ ta có
1) $k\left( {l\overrightarrow a } \right) = \left( {kl} \right)\overrightarrow a $
2) $\left( {k + l} \right)\overrightarrow a = k\overrightarrow a + l\overrightarrow a $
3) $k\left( {\overrightarrow a + \overrightarrow b } \right) = k\overrightarrow a + k\overrightarrow b ;\,\,k\left( {\overrightarrow a - \overrightarrow b } \right) = k\overrightarrow a - k\overrightarrow b $
4) $k\overrightarrow a = \overrightarrow 0 $ khi và chỉ khi k = 0 hoặc $\overrightarrow a = 0$
CHÚ Ý:
1) Do tính chất 1 ,ta có $\left( { - k} \right)\overrightarrow a = \left( { - 1} \right)\left( {k\overrightarrow a } \right) = - \left( {k\overrightarrow a } \right)$. Bởi vậy cả hai vectơ $\left( { - k} \right)\overrightarrow a $ và $ - \left( {k\overrightarrow a } \right)$đều có thể viết đơn giản là $ - k\overrightarrow a $
2) Vectơ $\frac{m}{n}\overrightarrow a $ có thể viết là $\frac{{m\overrightarrow a }}{n}$. Chẳng hạn $\frac{1}{3}\overrightarrow a $ có thể viết là $\frac{{\overrightarrow a }}{3}$
Bài toán 1:
Chứng minh rằng điểm I là trung điểm của đoạn thẳng AB khi và chỉ khi với điểm M bất kỳ, ta có $\overrightarrow {MA} \, + \overrightarrow {MB} \, = 2\,\overrightarrow {MI} $
Giải:
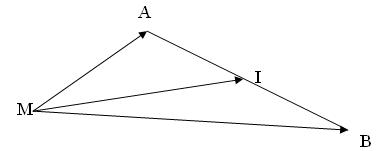
Với điểm M bất kì, ta có:
$\overrightarrow {MA} = \overrightarrow {MI} \, + \overrightarrow {IA} $
$\overrightarrow {MB} = \overrightarrow {MI} \, + \overrightarrow {IB} $
Như vậy
$\overrightarrow {MA} \, + \overrightarrow {MB} \, = 2\,\overrightarrow {MI} + \overrightarrow {IA} + \overrightarrow {IB} $
Ta biết rằng I là trung điểm của AB khi và chỉ khi $\overrightarrow {IA} \, + \overrightarrow {IB} \, = \overrightarrow 0 $. Từ đó suy ra điều phải chứng minh.
3. Điều kiện để hai vectơ cùng phương
Vectơ $\overrightarrow b $ cùng phương với vectơ $\overrightarrow a $($\overrightarrow a \ne 0$) khi và chỉ khi có số k sao cho $\overrightarrow b = k\overrightarrow a $
Điều kiện để ba điểm thẳng hàng
Điều kiện cần và đủ để ba điểm phân biệt A, B ,C thẳng hàng là có số k sao cho $\overrightarrow {AB} = k\overrightarrow {AC} $.
4. Biểu thị một vectơ qua hai vectơ không cùng phương
Định lí
Cho hai vectơ không cùng phương $\overrightarrow a $ và $\overrightarrow b $. khi đó mọi vectơ $\overrightarrow x $ đều có thể biểu thị được một cách duy nhất qua hai vectơ $\overrightarrow a $ và $\overrightarrow b $, nghĩa là có duy nhất cặp số m và n sao cho $\overrightarrow x = m\overrightarrow a + n\overrightarrow b $.
|