|
|
1. Khái niệm hàm số mũ và hàm số lôgarit
ĐỊNH NGHĨA
Gỉa sử $a$ là một số dương và khác $1$.
Hàm số dạng $y = {a^x}$ được gọi là hàm số mũ cơ số $a$
Hàm số dạng $y = {\log _a}x$ được gọi là hàm số lôgarit cơ số $a$
2. Một số giới hạn liên quan đến hàm số mũ và hàm số lôgarit
a) Ta thừa nhận rằng các hàm số $y = {a^x}$và $y = {\log _a}x$ liên tục tại mọi điểm mà nó xác định, tức là
$\begin{gathered}
\forall {x_o} \in \mathbb{R},\,\,\,\mathop {\lim }\limits_{x \to {x_0}} {a^x} = {a^{{x_0}}}, \\
\forall {x_o} \in \mathbb{R}_ + ^*,\,\,\,\mathop {\lim }\limits_{x \to {x_0}} {\log _a}x = {\log _a}{x_0}, \\
\end{gathered} $
a) Đạo hàm của hàm số lôgarit
Ta có: $\mathop {\lim }\limits_{x \to 0} {\left( {1 + x} \right)^{\frac{1}{x}}} = e\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,(1)$
Từ đó suy ra các giới hạn quan trọng sau:
ĐỊNH LÝ 1
$\begin{gathered}
\mathop {\lim }\limits_{x \to 0} \frac{{\ln (1 + x)}}{x} = 1\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,(2) \\
\mathop {\lim }\limits_{x \to 0} \frac{{{e^x} - 1}}{x} = 1\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,(3) \\
\end{gathered} $
3. Đạo hàm của hàm số mũ và hàm số lôgarit
a, Đạo hàm của hàm số mũ
ĐỊNH LÝ 2
a, Hàm số $y = {a^x}$ có đạo hàm tại mọi điểm $x \in \mathbb{R}$ và
$\left( {{a^x}} \right)' = {a^x}\ln a$ nói riêng ta có $\left( {{e^x}} \right)' = {e^x}$
b, Nếu hàm số $u = u(x)$ có đạo hàm trên $J$ thì hàm số $y = {a^{u(x)}}$ có đạo hàm trên $J$ và $\left( {{a^{u(x)}}} \right)' = u'(x){a^{u(x)}}\ln a$ nói riêng ta có $\left( {{e^{u(x)}}} \right)' = u'(x){e^{u(x)}}$
b, Đạo hàm của hàm số lôgarit
ĐỊNH LÍ 3
a, Hàm số $y = {\log _a}x$ có đạo hàm tại mọi điểm $x > 0$ và
$\left( {{{\log }_a}x} \right)' = \frac{1}{{x\ln a}}$; nói riêng ta có$\left( {\ln x} \right)' = \frac{1}{x}$
b, Nếu hàm số $u = u(x)$ nhận giá trị dương và có đạo hàm trên J thì hàm số $y = {\log _a}u(x)$có đạo hàm trên J và
$\left( {\log u(x)} \right)' = \frac{{u'(x)}}{{u(x)\ln a}}$ nói riêng ta có $\left( {\ln u(x)} \right)' = \frac{{u'(x)}}{{u(x)}}$
HỆ QUẢ
a) $\left( {\ln \left| x \right|} \right)' = \frac{1}{x}$ với mọi $x \ne 0$
b) Nếu hàm số $u = u(x)$ nhận giá trị khác 0 và số đạo hàm trên $J$ thì
$\left( {\ln \left| {u(x)} \right|} \right)' = \frac{{u'(x)}}{{u(x)}}$ với mọi $x \in J$
4. Sự biến thiên và đồ thị của hàm số mũ và hàm số lôgarit
a) Hàm số $y = {a^x}$
GHI NHỚ
Hàm số $y = {a^x}$
* Có tập xác định là $\mathbb{R}$và tập giá tri giá khoảng $(0; + \infty )$
* Đồng biến trên $\mathbb{R}$ khi a > 1 nghịch biến trên $\mathbb{R}$ khi $0 < a < 1$.
*Có đồ thị
- Đi qua điểm $( 0 ;1)$
- Nằm ở phía trên trục hoành,
- Nhận trục hoành làm tiệm cận ngang.
Đồ thị có một trong hai dạng nêu ở hình vẽ dưới đây:
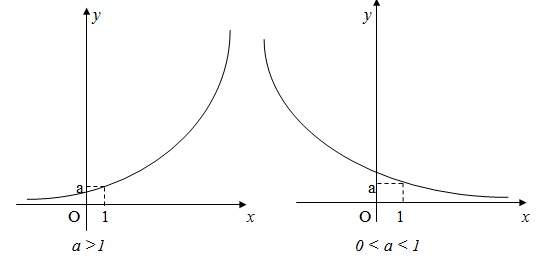
b. Hàm số $y = {\log _a}x$
Bảng kết quả khảo sát hàm số$y = {\log _a}x$ trang 108
GHI NHỚ:
Hàm số $y = {\log _a}x$
• Có tập hợp xác định là khoảng $(0; + \infty )$ và tập giá trị là $\mathbb{R}$
• Đồng biến trên khoảng $(0; + \infty )$khi a > 1 , nghịch biến trên $(0; + \infty )$ khi $0 < a < 1$;
• Có đồ thị
- Đi qua điểm $(1 ;0 )$,
- Nằm ở bên phải trục tung,
- Nhận trục tung làm tiệm cận đứng
|