|
|
1,Công thức nhị thức Niu-tơn (gọi tắt là nhị thức Niu-tơn)
${\left( {a + b} \right)^n} = C_n^0{a^n} + C_n^1{a^{n - 1}}b + ... + C_n^k{a^{n - k}}{b^k} + ... + C_n^n{b^n}$
$ = \sum\limits_{k = 0}^n {C_n^k{a^{n - k}}{b^k}} $ (Quy ước ${a^0} = {b^0} = 1$)
Ví dụ 1: Tính hệ số của ${x^{12}}{y^{13}}$ trong khai triển ${\left( {x + y} \right)^{25}}$
Giải: Theo công thức nhị thức Niu-tơn, hệ số này là $C_{25}^{13} = \frac{{25!}}{{13!.12! }}= 5200300$
Ví dụ 2: Tìm hệ số của ${x^3}$ trong khai triển ${\left( {3x - 4} \right)^5}$
Giải: Ta có ${\left( {3x - 4} \right)^5} = {\left( {3x + \left( { - 4} \right)} \right)^5}$. Theo công thức nhị thức Niu-tơn, số hạng chứa ${x^3}$ là $C_5^2{\left( {3x} \right)^3}.{\left( { - 4} \right)^2}$. Vậy hệ số của ${x^3}$ là ${10.3^3}.{\left( { - 4} \right)^2} = 4320$
2, Tam giác Pa-xcan
Trên đây ta muốn khai triển ${\left( {a + b} \right)^n}$ thành đa thức, ta cần biết $n + 1$ số $C_n^0,C_n^1,C_n^1,...,C_n^{n - 1},C_n^n$ có mặt trong công thức nhị thức Niu-tơn. Các số này có thể tính được nhờ sử dụng bảng số sau đây
..........................................................................
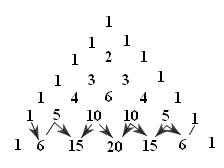
Tam giác Pa-xcan được lập theo quy luật sau:
• Đỉnh được ghi số 1. Tiếp theo là hàng thứ nhất ghi số 1.
• Nếu biết hàng thứ $n\left( {n \geqslant 1} \right)$ thì hàng thứ $n + 1$ tiếp theo được thiết lập bằng cách cộng hai số liên tiếp của hàng thứ $n$ rồi viết kết quả xuống hàng dưới ở vị trí giữa hai số này. Sau đó viết số 1 ở đầu và cuối hàng.
Chẳng hạn, khi có hàng thứ năm ta thiết lập hàng thứ sáu như sau: Theo thứ tự từ trái sang phải, ta lấy $1 + 5 = 6$ và viết số 6 xuống hàng dưới ở vị trí giữa số 1 và số 5; lấy 5+10=15 và viết số 15 xuống hàng dưới ở vị trí giữa hai số 5 và số 10… (Xem hình vẽ)
Nhận xét:
Xét hàng thứ nhất, ta có
$1 = C_1^0$, $1 = C_1^1$
Ở hàng thứ hai, ta có
$1 = C_2^0$, $2 = C_2^1$ $1 = C_2^2$
Ở hàng thứ ba, ta có
$1 = C_3^0$ $3 = C_3^1$ $3 = C_3^2$ $1 = C_3^3$
Một cách tổng quát, từ tính chất thứ 2 của số …(Hằng đẳng thức Pa-xcan) và một cách thiết lập tam giác Pa-xcan, ta có
Các số ở hàng thứ $n$trong tam giác Pa-xcan là dãy gồm $n + 1$ số
$C_n^0,C_n^1,C_n^2,...,C_n^{n - 1},C_n^n$
|