|
|
1. Đường tròn lượng giác
a, Định nghĩa
ĐỊNH NGHĨA
Đường tròn lượng giác là một đường tròn đơn vị (bán kính bằng l), định hướng, trên đó có một điểm A gọi là điểm gốc.
b, Tương ứng giữa số thực và điểm trên đường tròn lượng giác
Điểm M thuộc đường tròn lượng giác sao cho $\left( {OA,OM} \right) = \alpha $gọi là điểm xác định bởi số $\alpha $(hay bởi cung $\alpha $, hay bởi góc $\alpha $). Điểm M còn được gọi là điểm trên đường tròn lượng giác biểu diễn cung (góc) lượng giác có số đo $\alpha $.
Ta nhận xét ngay rằng
Ứng với mỗi số thực $\alpha $ có một điểm trên đường tròn lượng giác (điểm xác định bởi số đó) tương tự như trên trục số. Tuy nhiên, mỗi điểm trên đường tròn lượng giác ứng với vô số số thực. Các số thực đó có dạng $\alpha + k2\pi ,\,\,k \in \mathbb{Z}$.
c, Hệ tọa độ vuông góc gắn với đường tròn lượng giác.
Cho đường tròn lượng giác tâm O, điểm gốc A. Xét hệ tọa độ vuông góc Oxy sao cho tia Ox trùng với tia OA, góc lượng giác (Ox, Oy) là góc $\frac{\pi }{2} + k2\pi ,\,\,k \in \mathbb{Z}$.Hệ tọa độ đó được gọi là hệ tọa độ vuông góc gắn với đường tròn lượng giác đã cho.

Sau này, ta luôn xét đường tròn lượng giác trong hệ tọa độ vuông góc gắn với nó.
2. Giá trị lượng giác sin và côsin
a, Các định nghĩa
Với mỗi góc lượng giác (Ou, Ov) có số đo $\alpha $, lấy điểm M trên đường tròn lượng giác để $(OA,OM) = \alpha $, tức là điểm M xác định bởi số $\alpha $. Gọi tọa độ của M trong hệ tọa độ gắn với đường tròn đó là $(x;y)$
Hoành độ x của M được gọi là côsin của góc lượng giác (Ou, Ov) hay của$\alpha $ và kí hiệu
$c{\text{os}}(Ou,Ov) = c{\text{os}}\alpha = x$
Tung độ y của M được gọi là sin của góc lượng giác (Ou, Ov) hay của $\alpha $ và kí hiệu
$\sin (Ou,Ov) = \sin \alpha = y$
Nếu $s{\text{d}}(Ou,Ov) = {a^0}$ thì ta cũng viết
$\begin{gathered}
c{\text{os(}}Ou,Ov) = c{\text{os}}{{\text{a}}^0} \\
\sin (Ou,Ov) = \sin \,{{\text{a}}^0} \\
\end{gathered} $
CHÚ Ý
Gọi $\overrightarrow i = \overrightarrow {OA} ,\,\,\overrightarrow j = \overrightarrow {OB} $là các vectơ đơn vị trên trục hoành và trục tung
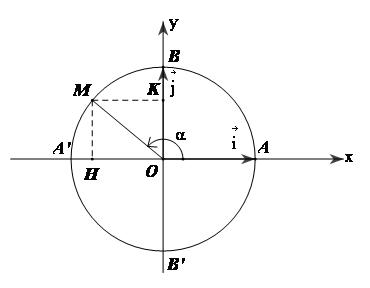
Khi đó nếu điểm M thuộc đường tròn lượng giác xác định bởi số $\alpha $ thì
$\overrightarrow {OM} = (c{\text{os}}\alpha )\overrightarrow i + (\sin \alpha )\,\overrightarrow j $
Tức là M có tọa độ $(c{\text{os}}\alpha ;\sin \alpha )\,$
Gọi H, K theo thứ tự là hình chiếu vuông góc của điểm M trên Ox và Oy thì $\overrightarrow {OH} = (c{\text{os}}\alpha )\overrightarrow i $ và $\overrightarrow {OK} = (\sin \alpha )\,\overrightarrow j $, tức là:
$c{\text{os}}\alpha = \overline {OH} \,\,\,;\,\,\,\sin \alpha = \overline {OK} $
Trong lượng giác, người ta còn gọi trục Ox là trục côsin và trục Oy là trục sin.
b, Tính chất
1, Vì các góc lượng giác $\alpha + k2\pi ,\,\,k \in \mathbb{Z}$cùng xác định một điểm M trên đường tròn lượng giác nên ta có
$c{\text{os(}}\alpha + k2\pi ) = c{\text{os}}\alpha \,\,\,;\,\,\,\sin (\alpha + k2\pi ) = \sin \alpha $
2, Với mọi $\alpha $, ta luôn có
$ - 1 \leqslant c{\text{os}}\alpha \leqslant 1\,\,\,;\,\,\, - 1 \leqslant \sin \alpha \leqslant 1$
3, Vì $O{H^2} + O{K^2} = O{M^2} = 1$ nên ta có $c{\text{o}}{{\text{s}}^2}\alpha + {\sin ^2}\alpha = 1$

3. Giá trị lượng giác tang và côtang
a, Các định nghĩa
Cho góc lượng giác (Ou, Ov) có số đo $\alpha $.
Nếu $c{\text{os}}\alpha \,\, \ne \,\,0$(tức là $\alpha \,\, \ne \,\frac{\pi }{2} + k\pi ,k \in \mathbb{Z}$) thì tỉ số $\frac{{\sin \alpha }}{{c{\text{os}}\alpha }}$ được gọi là tang của góc $\alpha $, kí hiệu là tan$\alpha $ (người ta còn kí hiệu là \tan$\alpha $)
Vậy:
$\tan (Ou,Ov) = \tan \alpha = \frac{{\sin \alpha }}{{c{\text{os}}\alpha }}$
Nếu $\sin \alpha \,\, \ne \,\,0$(tức là $\alpha \,\, \ne \,k\pi ,k \in \mathbb{Z}$) thì tỉ số $\frac{{c{\text{os}}\alpha }}{{\sin \alpha }}$ được gọi là cô-tang của góc $\alpha $, kí hiệu là cot$\alpha $ (người ta còn kí hiệu là cot$\alpha $)
$\cot (Ou,Ov) = \cot \alpha = \frac{{c{\text{os}}\alpha }}{{\sin \alpha }}$$\tan (Ou,Ov) = \tan \alpha = \frac{{\sin \alpha }}{{c{\text{os}}\alpha }}$
b, Ý nghĩa hình học
- Xét trục số At gốc A, tiếp xúc với đường tròn lượng giác tại điểm gốc A và cùng hướng với trục Oy. Khi (OA, OM) = $\alpha $ sao cho $c{\text{os}}\alpha \ne 0$ thì đường thẳng OM cắt trục At tại điểm T có tọa độ là $\left( {1;\tan \alpha } \right)$, tức là:
$\tan \alpha = \overline {AT} $
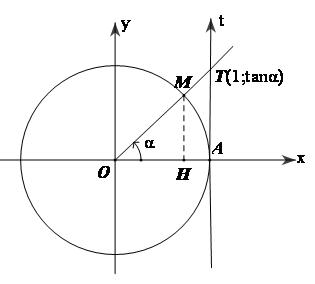
Thực vậy, đường thẳng qua gốc O (khác Oy) có phương trình y = kx nên nó đi qua điểm $M\left( {c{\text{os}}\alpha ;\sin \alpha } \right)$khi và chỉ khi $k = \frac{{\sin \alpha }}{{c{\text{os}}\alpha }}$. Vậy phương trình đường thẳng OM là $y = \frac{{\sin \alpha }}{{c{\text{os}}\alpha }}.x$ (hình vẽ). Rõ ràng giao điểm T đang xét có hoành độ x = 1 nên tung độ của T là $y = \frac{{\sin \alpha }}{{c{\text{os}}\alpha }} = \tan \alpha $
Vi vậy trục At còn gọi là trục tang.
- Xét trục số Bs gốc B, tiếp xúc với đường tròn lượng giác tại điểm B(0;1) và cùng hướng với trục Ox.
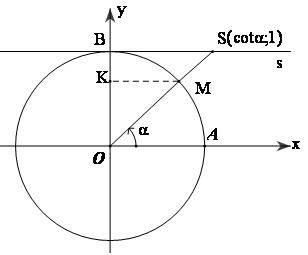
Khi (OA, OM) = $\alpha $ sao cho $\sin \alpha \ne 0$ thì đường thẳng OM cắt trục Bs tại điểm S có tọa độ là $\left( {\cot \alpha ;1} \right)$, tức là:
$\cot \alpha = \overline {BS} $
Chứng minh tương tự như trên.
Vi vậy trục At còn gọi là trục côtang.
c, Tính chất
1) Từ ý nghĩa hình học nói trên, suy ra: với mọi $k \in \mathbb{Z}$, ta có
$\tan (\alpha + k\pi ) = \tan \alpha ;\cot (\alpha + k\pi ) = \cot \alpha $
(khi các biểu thức có nghĩa)
2) Từ định nghĩa tang và côtang, suy ra
Khi $\sin \alpha ,\cos \alpha \ne 0$ (tức khi $\alpha \ne k\frac{\pi }{2},k \in \mathbb{Z}$), ta có$\cot \alpha = \frac{1}{{\tan \alpha }}$
3) Từ định nghĩa tang và côtang và từ công thức${\sin ^2}\alpha + c{\text{o}}{{\text{s}}^2}\alpha = 1$ , ta suy ra ngay các công thức;
Khi $\cos \alpha \ne 0$, $1 + {\tan ^2}\alpha = \frac{1}{{c{\text{o}}{{\text{s}}^2}\alpha }}$
Khi $\sin \alpha \ne 0$, $1 + {\cot ^2}\alpha = \frac{1}{{{{\sin }^2}\alpha }}$
4, Tìm giá trị lượng giác của một số góc
Từ định nghĩa các giá trị lượng giác nói trên, ta thấy: Nếu góc lượng giác (Ou, Ov) có số đo $\alpha $, $0 \leqslant \alpha \leqslant \pi $ thì các giá trị lượng giác của nó bằng các giá trị lượng giác của góc hình học uOv đã học trước đây: Ta có bảng sau:
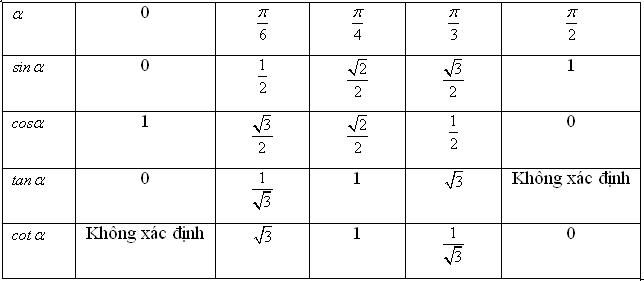
- Khi biết một giá trị lượng giác của góc $\alpha $, có thể dùng các công thức lượng giác ở mục 2, mục 3 và dấu của giá trị lượng giác để tính toán các giá trị lượng giác còn lại của góc $\alpha $.
Ví dụ: Cho $\alpha ,\pi < \alpha < \frac{{3\pi }}{2}$. Hãy tìm $c{\text{os}}\alpha $ nếu biết ${\text{sin}}\alpha \, = \frac{4}{5}$
Giải: Do $\pi < \alpha < \frac{{3\pi }}{2}$ nên $c{\text{os}}\alpha < 0$, từ đó:
$c{\text{os}}\alpha = - \sqrt {1 - {{\sin }^2}\alpha } = - \frac{3}{5}$
CHÚ Ý
Vì cho góc lượng giác (Ou, Ov) cũng có nghĩa là cho cung lượng giác tương ứng trên đường tròn lượng giác tâm O, nên nói về các giá trị lượng giác của góc (Ou, Ov) cũng có nghĩa là nói về các giá trị lượng giác của cung tương ứng.
|