|
|
1. Giải và biện luận phương trình dạng ax+b=0
Kết quả giải và biện luận phương trình dạng ax+b=0 được nêu trong bảng sau đây:
1) a≠0: Phương trình có một nghiệm duy nhất x=−ba
2) a=0&b≠0: Phương trình vô nghiệm
3)a=0&b=0: Phương trình nghiệm đúng với mọi x∈R
2. Giải và biện luận phương trình dạng ax2+bx+c=0
Kết quả giải và biện luận phương trình dạng ax2+bx+c=0được nêu trong bảng sau đây:
1)a=0: Trở về giải và biện luận phương trình bx + c = 0
2)a≠0:
Δ>0: phương trình có hai nghiệm (phân biệt)
x1=−b−√Δ2a và x2=−b+√Δ2a
Δ=0: phương trình có một nghiệm kép x1=x2=−b2a
Δ<0: phương trình vô nghiệm
Ví dụ: Cho phương trình
3x+2=−x2+x+a (3)
Bẳng đồ thị, hãy biện luận số nghiệm của phương trình (3) tùy theo các giá trị của tham số a
Giải
Trước hết, ta đưa phương trình (3) về dạng
x2+2x+2=a (4)
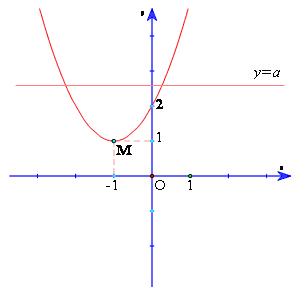
Số nghiệm của phương trình (3) cũng là số nghiệm của phương trình (4) và bằng số giao điểm của parabol (P): y=x2+2x+2với đường thẳng(d):y=a. Quan sát đồ thị ta thấy đỉnh của parabol (P) là điểm M(-1; 1), khi a thay đổi thì đường thẳng (d) cũng thay đổi nhưng luôn song song (hoặc trùng) với trục hoành. Từ đó, suy ra:
Với a<1, phương trình (3) vô nghiệm ( đường thẳng (d) và parabol (P) không có điểm chung)
Với a = 1, phương trình (3) có một nghiệm kép (đường thẳng (d) tiếp xúc với parabol (P))
Với a>1, phương trình (3) có hai nghiệm phân biệt (đường thẳng (d) cắt parabol (P) tại hai điểm phân biệt)
CHÚ Ý
Khi viết phương trình (3) dưới dạng x2+2x+2=a, ta thấy kết quả trên còn cho biết số giao điểm của parabol y=x2+3x+2với đường thẳng y=x+a.
3. Ứng dụng của định lý Vi – ét
Hai số x1&x2 là các nghiệm của phương trình bậc hai
ax2+bx+c=0
Khi và chỉ khi chúng thỏa mãn các hệ thức:
x1+x2=−ba&x1x2=ca
Định lý Vi – ét có nhiều ứng dụng quan trọng, chẳng hạn như:
1) Nhẩm nghiệm của phương trình bậc hai;
2) Phân tích đa thức thành nhân tử;
Nếu đa thức f(x)=ax2+bx+ccó hai nghiệm x1&x2 thì nó có thể phân tích thành nhân tử f(x)=a(x−x1)(x−x2)
3) Tìm hai số biết tổng và tích của chúng;
Nếu hai số có tổng là S và tích là P thì chúng là các nghiệm của phương trình x2−Sx+P=0.
Ta có ứng dụng quan trọng khác của định lý Vi – ét là xét dấu các nghiệm của phương trình bậc hai.
NHẬN XÉT
Cho phương trình bậc hai ax2+bx+c=0 có hai nghiệm x1&x2 (x1⩽x2). Đặt S=−bavà P=ca. Khi đó:
- Nếu P < 0 thì x1<0<x2 (hai nghiệm trái dấu);
- Nếu P > 0 và S > 0 thì 0<x1⩽x2(hai nghiệm dương);
- Nếu P > 0 và S < 0 thì x1⩽x2<0(hai nghiệm âm);
Ví dụ:
Xét dấu các nghiệm của phương trình sau (nếu có)
(2−√3)x2+2(1−√3)x+1=0 (*)
Giải
Ta có
a=2−√3>0 và c=1>0⇒P>0
Δ′=(1−√3)2−(2−√3)=(2−√3)⇒Δ′>0(vậy (*) có hai nghiệm phân biệt)
a=2−√3>0 và −b=−2(1−√3)=2(√3−1)>0⇒S>0
Do đó, phương trình đã cho có hai nghiệm dương
|