|
|
1. Khái niệm về hàm số
a, Hàm số
ĐỊNH NGHĨA
Cho một tập hợp khác rỗng $D \subset \mathbb{R}$
Hàm số f xác định trên D là một quy tắc đặt tương ứng mỗi số x thuộc D với một và chỉ một số, kí hiệu là $f\left( x \right)$; số $f\left( x \right)$ đó gọi là giá trị của hàm số f tại x.
Tập D gọi là tập xác định (hay miền xác định), x là gọi là biến số hay đối số của hàm số f
Để chỉ rõ ký hiệu biến số, hàm f còn được viết là $y = f\left( x \right)$, hay đầy đủ hơn là
$\begin{gathered}
f:D \to \mathbb{R} \end{gathered} $
$\begin{gathered} x \mapsto y = f\left( x \right)
\end{gathered} $
b, Hàm số cho bằng biểu thức
Nếu f(x) là một biểu thức của biến x thì với mỗi giá trị của x, ta tính được một giá trị tương ứng duy nhất của f(x) (nếu nó xác định). Do đó, ta có hàm số y=f(x). Ta nói hàm số đó được cho bằng biểu thức f(x)
Khi cho hàm số được cho bằng biểu thức, ta quy ước rằng:
Nếu không có giải thích gì thêm thì tập xác định của hàm $y=f(x)$ là tập hợp tất cả các số thực $x$ sao cho giá trị của biểu thức $f(x)$ được xác định.
CHÚ Ý
Trong kí hiệu $y=f(x)$, ta còn gọi $x$ là biến số độc lập, $y$ là biến số phụ thuộc của hàm số $f$. Biến số độc lập và biến số phụ thuộc của một hàm số có thể được kí hiệu bởi hai chữ cái tùy ý khác nhau. Chẳng hạn,$y = {x^2} - 2x - 3$ và $u = {t^2} - 2t - 3$
là hai cách viết biểu thị cùng một hàm số.
c, Đồ thị của hàm số
Cho hàm số $y = f\left( x \right)$xác định trên tập$ D$. Ta đã biết trong mặt phẳng tọa độ $(Oxy)$, tập hợp $(G)$ các điểm có tọa độ $\left( {x;f\left( x \right)} \right)$với $x \in D$, gọi là đồ thị của hàm số f. Nói cách khác,
$M\left( {{x_0};{y_0}} \right) \in (G) \Leftrightarrow {x_0} \in D\,$và ${y_0} = f({x_0})$
Qua đồ thị của một hàm số, ta có thể nhận biết được nhiều tính chất của hàm số đó.

2. Sự biến thiên của hàm số
a, Hàm số đồng biến, hàm số nghịch biến
Khi nghiên cứu một hàm số, người ta thường quan tâm đến sự tăng hay giảm của giá trị hàm số khi đối số tăng.
Ví dụ 3: Xét hàm số $f(x) = {x^2}$. Gọi $ x_{1} $ và $x_{2} $ là hai giá trị tùy ý của đối số
Trường hợp 1: Khi $ x_{1} $ và $x_{2} $ thuộc nửa khoảng ${\text{[}}0; + \infty )$, ta có
$0 \leqslant {x_1} < {x_2} \Rightarrow x_1^2 < x_2^2 \Rightarrow f({x_1}) < f({x_2})$
Trường hợp 2: Khi $ x_{1} $ và $x_{2} $ thuộc nửa khoảng $( - \infty ;0]$, ta có
${x_1} < {x_2} \leqslant 0 \Rightarrow |x_1^{}| > |x_2^{}| \Rightarrow x_1^2 > x_2^2 \Rightarrow f({x_1}) > f({x_2})$
ĐỊNH NGHĨA
Cho hàm số f xác định trên K
Hàm số f gọi là đồng biến (hay tăng) trên K nếu
$ \forall x_{1}, x_{2} \in K , x_{1}< x_{2} \Rightarrow f(x_{1})< f(x_{2}) $
Hàm số f gọi là nghịch biến (hay giảm) trên K nếu
$\forall {x_1},{x_2} \in K,{x_1} < {x_2} \Rightarrow f({x_1}) > f({x_2})$
Tổng quát, ta có:
Nếu một hàm số đồng biến trên K thì trên đó, đồ thị của nó đi lên từ trái qua phải;
Nếu một hàm số nghịch biến trên K thì trên đó, đồ thị của nó đi xuống từ trái qua phải
CHÚ Ý
Nếu $f({x_1}) = f({x_2})$ với mọi $x_{1}, x_{2} \in K $, tức là $f(x) = c$với mọi $x \in K$ $c $ là hằng số) thì ta có hàm số không đổi (còn gọi là hàm số hằng) trên $K$.
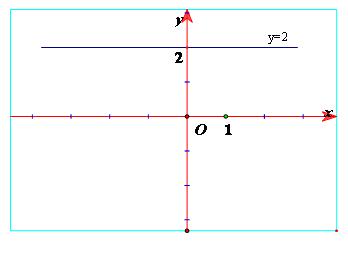
Chẳng hạn, $y=2$ là một hàm số không đổi xác định trên $\mathbb{R}$. Nó có đồ thị là trục song song với $Ox$
b, Khảo sát sự biến thiên của hàm số
Khảo sát sự biến thiên của hàm số là xét xem hàm số đồng biến, nghịch biến, không đổi trên các khoảng (nửa khoảng hay đoạn) nào trong tập xác định của nó
Do đó
Hàm số $f$ đồng biến trên $K$ khi và chỉ khi
$\forall {x_1},{x_2} \in K, \frac{f(x_{1} )-f(x_{2} )}{{x_1}-{x_2}}>0 $
Hàm số f nghịch biến trên K khi và chỉ khi
$\forall {x_1},{x_2} \in K, \frac{f(x_{1} )-f(x_{2} )}{{x_1}-{x_2}}<0 $
3. Hàm số chẵn, hàm số lẻ
a, Khái niệm hàm số chẵn, hàm số lẻ
ĐỊNH NGHĨA
Cho hàm số $y = f\left( x \right)$với tập xác định D
Hàm số f gọi là hàm số chẵn nếu với mọi x thuộc D , ta có –x cũng thuộc D và $f\left( { - x} \right) = f\left( x \right)$
Hàm số f gọi là hàm số lẻ nếu với mọi x thuộc D , ta có –x cũng thuộc D và $f\left( { - x} \right) = - f\left( x \right)$
b, Đồ thị của hàm số chẵn và hàm số lẻ
ĐỊNH LÝ
Đồ thị của hàm số chẵn nhận trục tung làm trục đối xứng. Đồ thị của hàm số lẻ nhận gốc tọa độ làm tâm đối xứng.
4. Sơ lược về tịnh tiến đồ thị song song với trục tọa độ
a, Tịnh tiến một điểm
Trong mặt phẳng tọa độ, xét điểm ${M_0}\left( {{x_0};{y_0}} \right)$. Với số k>0 đã cho ta có thể dịch chuyển điểm $M_{0} $:
- Lên trên hoặc xuống dưới (theo phương của trục tung) $k$ đơn vị;
- Sang trái hoặc sang phải (theo phương của trục hoành) $k$ đơn vị;
Khi dịch chuyển điểm $M_{0} $ như thế, ta còn nói rằng tịnh tiến điểm $M_{0} $ song song với trục tọa độ
b, Tịnh tiến trục đồ thị
Tịnh tiến đồ thị $(G)$ lên trên $k$ đơn vị thì được hình $(G1)$, hoặc hình $(G1)$ có được khi tịnh tiến $(G)$ lên trên $k$ đơn vị $( k > 0)$
ĐỊNH LÝ
Trong mặt phẳng tọa độ $(Oxy)$, cho đồ thị $(G)$ của hàm số $y = f(x)$; p và q là hai số dương tùy ý. Khi đó:
1) Tịnh tiến $(G)$ lên trên $q$ đơn vị thì được đồ thị của hàm số $y = f(x) + q$
2) Tịnh tiến $(G)$ xuống dưới $q$ đơn vị thì được đồ thị của hàm số $y = f(x) - q$
3) Tịnh tiến $(G)$ sang trái $p$ đơn vị thì được đồ thị của hàm số $y = f(x + p)$
4) Tịnh tiến $(G)$ sang phải $p$ đơn vị thì được đồ thị của hàm số $y = f(x - p)$
Ví dụ:
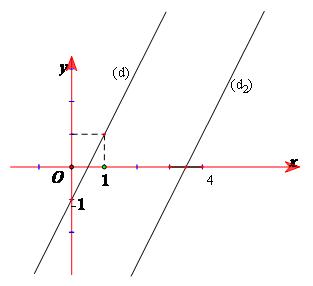
Nếu tịnh tiến đường thẳng (d) $y = 2x - 1$sang phải 3 đơn vị thì ta được đồ thị của hàm số nào?
Giải
Ký hiệu $f\left( x \right) = 2x - 1$. Theo định lý trên, khi tịnh tiến (d) sang phải 3 đơn vị, ta được (d1), đó là đồ thị của hàm số
$y = f\left( {x - 3} \right) = 2(x - 3) - 1$
Tức là hàm số $y = 2x - 7$
|