|
|
1. Các hàm số y = sinx và y=cosx
a) Định nghĩa
Quy tắc đặt tương ứng mỗi số thực x với sin của góc lượng giác có số đo radian bằng x được gọi là hàm số sin, kí hiệu là y = sin x.
Quy tắc đặt tương ứng mỗi số thực x với côsin của góc lượng giác có số đo radian bằng x được gọi là hàm số cosin, kí hiệu là y = cos x.
Tập xác định của các hàm số y = sin x, y = cos x là . Do đó các hàm số sin và cosin được viết tắt là:
sin: R→R cos: R→R
x → sin x x → cos x
Nhận xét: Hàm số y = sinx là một hàm số lẻ vì sin(-x) = - sin(x) ∀x∈R
b) Tính chất tuần hoàn của các hàm số y = sin x và y = cos x
Ta chứng minh được hàm số y = sinx, số 2π là số dương nhỏ nhất thỏa mãn sin(x+T)=sin x với mọi x.
Hàm số y = cos x cũng có tính chất tương tự. Ta nói hai hàm số đó là những hàm số tuần hoàn với chu kỳ 2π. Khi đó, khi biết giá trị của hàm số trên một đoạn có độ dài 2π thì ta tính được giá trị của chúng tại mọi điểm.
c) Sự biến thiên và đồ thị của hàm số y = sinx
Chiều biến thiên ( xem hình )
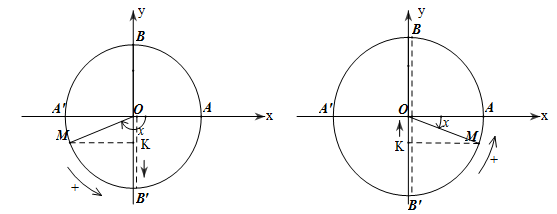

Khi x tăng từ -π đến -π2, sinx giảm từ 0 đến -1.
Khi x tăng từ -π2 đến π2 thì sinx tăng từ -1 đến 1.
Khi x tăng từ π2 đến π , sin x giảm từ 1 đến 0
Đồ thị :
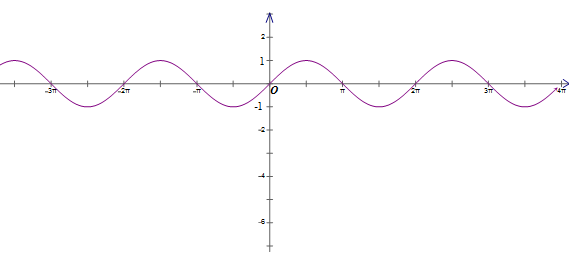
Nhận xét
1) Khi x thay đổi, hàm số y = sin x nhận mọi giá trị thuộc đoạn [-1;1]. Ta nói tập giá trị của hàm số y = sinx là đoạn [-1;1]
2) Hàm số y = sinx đồng biến trên khoảng (−π2;π2). Từ đó, do tính chất tuần hoàn với chu kỳ 2π, hàm số y = sin x đồng biến trên mỗi khoảng (−π2+k2π;π2+k2π),k∈Z .
d) Sự biến thiên và đồ thị của hàm số y = cos x
Đồ thị hàm cosx là một đường vẽ bằng cách tịnh tiến đồ thị hàm số y = sin x sang trái 1 đoạn có độ dài π2
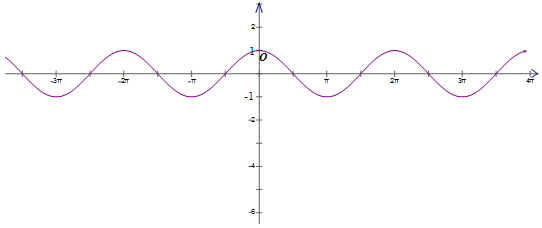
Nhận xét: Tập giá trị của hàm y=cos x là đoạn [-1;1]
Đồ thị hàm số y = cos x nhận trục tung làm trục đối xứng
Hàm số y = cosx đồng biến trên mỗi khoảng (−π+k2π;k2π),k∈Z
2. Các hàm số y = tanx và y = cotx
a) Định nghĩa
- Quy tắc đặt tương ứng mỗi số x∈D1 với số thực tan x = sinxcosx được gọi là hàm số tang, ký hiệu y = tan x.
- Quy tắc đặt tương ứng mỗi số x ∈D2 với số thực cot x = cosxsinx được gọi là hàm số cotang, ký hiệu là y = cot x.
tan: D1→R cot: D2 →R
x → tan x x → cot x
|
Hàm số y = tanx
|
Hàm số y = cot x
|
|
-
Có tập xác định
là
D1=R∖{π2+kπ|k∈Z}
-
Có tập giá trị
là R
-
Là hàm số lẻ
-
Là hàm số tuần
hoàn với chu kỳ π
-
Đồng biến trên
mỗi khoảng (−π2+kπ;π2+kπ),k∈Z
-
Có đồ thị nhận
mỗi đường thẳng x=π2+kπ(k∈Z) làm một đường tiệm
cận.
|
-
Có tập xác định
là
D2=R∖{kπ|k∈Z}
-
Có tập giá trị
là R
-
Là hàm số lẻ
-
Là hàm số tuần
hoàn với chu kỳ π
-
Nghịch biến
trên mỗi khoảng (kπ;π+kπ),k∈Z
- Có đồ thị nhận mỗi đường
thẳng x=kπ(k∈Z) làm một đường tiệm
cận.
|
3. Về khái niệm hàm số tuần hoàn:
ĐN: Hàm số y = f(x) xác định trên tập hợp D được gọi là hàm số tuần hoàn nếu có số T≠0 sao cho với mọi x∈D ta có:
x+T∈D, x-T ∈D và f(x+T)=f(x)
Nếu có số dương nhỏ nhất thỏa mãn các điều kiện trên thì hàm số đó gọi là một hàm tuần hoàn với chu kỳ T.
|