Ta có ) (đường tròn tâm G bán kính GA) cắt đoạn MC tại duy nhất 1 điểm là D(1)
(đường tròn tâm G bán kính GA) cắt đoạn MC tại duy nhất 1 điểm là D(1)
_ Gọi D' là điểm thuộc đoạn MC: 
_ Gọi E là trung điểm AB, F là hình chiếu của D lên ME
_ Đặt độ dài 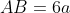
_ Ta lần lượt cm các điều sau:
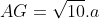
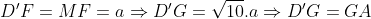
Suy ra D' là giao điểm của ) với đoạn MC (2)
với đoạn MC (2)
Từ (1) và (2) suy ra 
Xét hình thang vuông DFEA:  DG vuông góc với AG
DG vuông góc với AG