|
|
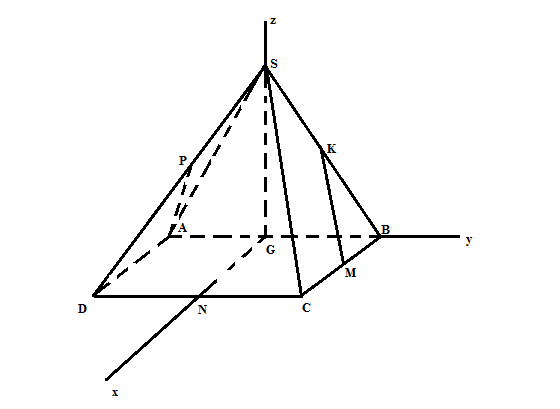
Gọi G và N lần lượt là trung điểm của AB, CD
Vì $\Delta$SAB là tam giác đều và mp(SAB) vuông góc với mp đáy => SG vuông góc với mp(ABCD)
Ta sẽ gắn hệ trục tọa độ vào hình vẽ sao cho G trùng với gốc O , GN trùng với Ox, GB trùng với Oy, GS trùng với Oz
Khi đó tọa độ các điểm là: M(a/2, a/2, 0); K(0,a/4, $\frac{a\sqrt{3}}{4}$) ; A(0, -a/2, 0); P(a/2, -a/4,$\frac{a\sqrt{3}}{4}$ )
Vậy khoảng cách giữa MK và AP là: h= $\frac{\left| {\left[ {\overrightarrow{MK}, \overrightarrow{AP}} \right].\overrightarrow{MA}} \right|}{\left| {\left[ {\overrightarrow{MK},\overrightarrow{AP}} \right]} \right|}$ = $\frac{3a}{2\sqrt{5}}$
|