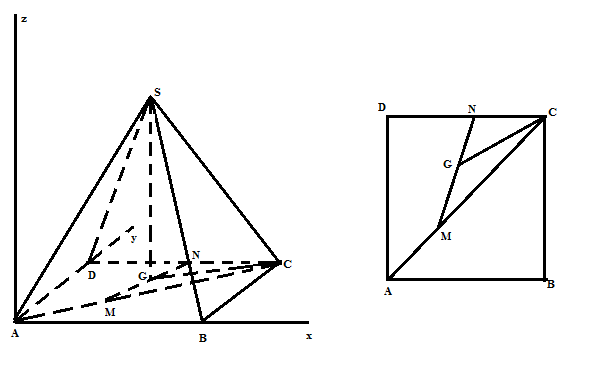
|
|
Gọi G là hình chiếu vuông góc của S xuống mp (ABCD) => ^SCG= 600
Gắn hình vẽ vào trong hệ trục tọa độ sao cho A trùng với gốc tọa độ, AB trùng với Ox, AD trùng với Oy, Oz là đường thẳng qua A và vuông góc với mp(ABCD)
Khi đó tọa độ các điểm là: M(a/3, a/3, 0); C(a,a, 0); D(0,a,0); N(a/2,a,0)
Có: G là trung điểm của MN => tọa độ G (5a/12, 2a/3, 0)
=> →GC (7a/12, a/3, 0) => GC= √65a12
Mà: ΔSGC vuông tại G => SG= GC. tan SCG= √195a12
=> Tọa độ S (5a12,2a3,√195a12)
Từ đó, ta có khoảng cách h giữa DM và SN là: h= |[→DM,→SN].→MN||[→DM,→SN]| = √195a5√43
|