|
|
a) $ \frac{4x^2+5x-1}{2x^2+5x+3}>1 \Leftrightarrow
\frac{4x^2+5x-1}{2x^2+5x+3}-1>0 \Leftrightarrow
\frac{x^2-2}{2x^2+5x+3}>0 $
$x^2-2$ có hai nghiệm $x=\pm \sqrt{2} $
$2x^2+5x+3$ có hai nghiệm $x=-1; x=-\frac{3}{2} $.
Bảng xét dấu:
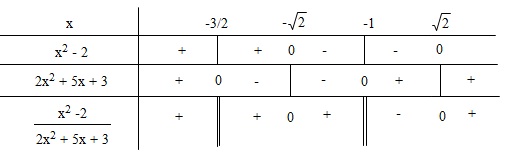
Nghiệm của bất phương trình là:
$S=\left\{ {x| x \in \mathbb{R} ; x<-\frac{3}{2}; -\sqrt{2}<x<-1; x> \sqrt{2} } \right\} $

b) $\frac{2x}{x+2}+\frac{x+2}{2x} \geq 4, x \neq -2, x \neq 0$.
$\Rightarrow \frac{2x}{x+2}+\frac{x+2}{2x}-4 \geq 0 \Rightarrow \frac{4x^2+(x+2)^2-8x(x+2)}{2x(x+2)} \ge 0$
$\Rightarrow \frac{-3x^2-12x+4}{2x(x+2)} \geq 0$.
Lập bảng xét dấu của phân thức vế trái.
Tam thức $-3x^2-12x+4$ có hai nghiệm $x=\frac{6 \pm 4 \sqrt{3} }{3} $.
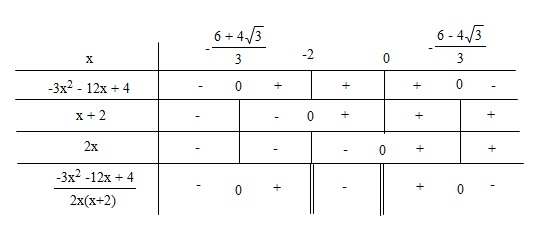
Nghiệm của bất phương trình là:
$S= \left\{ {x|x \in \mathbb{R}; -\frac{6+4 \sqrt{3} }{3} } \leq x <-2; 0<x \leq -\frac{6- 4 \sqrt{3} }{3} \right\} $

c) $ (x^2-x+5)^2<(x^2-3x+7)^2 \Leftrightarrow (x^2-x+5)^2-(x^2-3x+7)^2<0$
$\Leftrightarrow (x^2-2x+6)(x-1)<0$.
Tam
thức $x^2-2x+6$ có $\Delta'=1-6<0$ vì hệ số hạng tử chứa $x^2$
là $1>0$ nên $x^2-2x+6>0 \forall x, x \in \mathbb{R}$.
Bất phương trình trên tương đương với: $x-1<0 \Leftrightarrow x<1$
$S=\left\{ {x| x \in \mathbb{R}, x<1} \right\} $

|