|
|
|
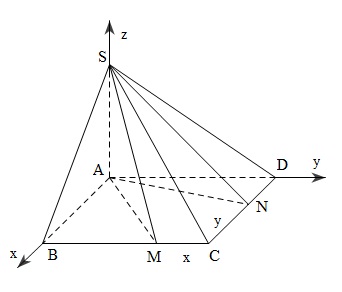 Chọn hệ trục tọa độ Axyz sao cho: A(0;0;0),B(a;0;0),C(a;a;0),D(0;a;0),S(0;0;h)M(a;a−x;0),N(a−y;a;0),0<x,y<aa) Ta có: {AS⊥AMAS⊥AN(doAS⊥(ABCD))⇒[M,AS,N]=(→AM,→AN)→AM=(a;a−x;0),→AN=(a−y;a;0)cos450=→AM,→AN|→AM|.|→AN|=a(a−y)+(a−x)a√(2a2−2ax+x2)(2a2−2ay+y2)⇔2a2(4a2+x2+y2−4ax−4ay+2xy)=(2a2−2ax+X2)(2a2−2ay+y2)Vậy hệ thức là 4a2−4a3(x+y)+2axy(x+y)−x2y2=0b) Tìm x,y để (SAM)⊥(SMN)Ta có: {(SAM)⊥(AMN)(SAM)⊥(SMN)⇒MN⊥(SAM)⇒ để (SAM)⊥(SMN) thì AM⊥MN⇒→AM.→MN=0⇒(a;a−x;0)(−y;x;0)=0⇔x2−ax+ay=0Vậy hệ thức là x2−ax+ay=0 |